【题目】如图,在平面直角坐标系xOy中,⊙A与y轴相切于点B(0, ![]() ),与x轴相交于M,N两点,如果点M的坐标为(
),与x轴相交于M,N两点,如果点M的坐标为( ![]() ,0),求点N的坐标
,0),求点N的坐标
参考答案:
【答案】解:连接AB、AM、过A作AC⊥MN于C,设⊙A的半径是R,

∵⊙A与y轴相切于B,
∴AB⊥y轴,
∵点B(0, ![]() ),与x轴相交于M、N两点,点M的坐标为(
),与x轴相交于M、N两点,点M的坐标为( ![]() ,0),
,0),
∴AB=AM=R,CM=R- ![]() ,AC=
,AC= ![]() ,MN=2CM,
,MN=2CM,
由勾股定理得:R2=(R- ![]() )2+(
)2+( ![]() )2,
)2,
R=2.5,
∴CM=CN=2.5- ![]() =2,
=2,
∴ON= ![]() +2+2=4
+2+2=4 ![]() ,
,
即N的坐标是(4 ![]() ,0).
,0).
【解析】要求点N的坐标,就需求出MN的长,因此过A作AC⊥MN于C,连接AB、AM、先由点B的坐标,就可求出AC的长,AB=OC=R,由点M的坐标就可求出OM的长,表示出MC的长,根据勾股定理求出R的长,即可求出MN的长,从而得出点N的坐标。
【考点精析】根据题目的已知条件,利用勾股定理的概念和垂径定理的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
∵
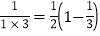 ,
,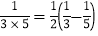 ,
,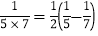 ,……
,……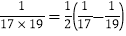 ,
,∴
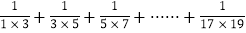
=
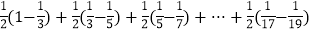
=
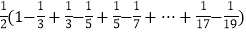 =
=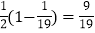 .
.解答下列问题:
(1)在和式
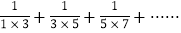 中,第6项为______,第n项是__________.
中,第6项为______,第n项是__________.(2)上述求和的想法是通过逆用分式减法法则,将和式中的各分数转化为两个数之差,使得除首末两项外的中间各项的和为_______,从而达到求和的目的.
(3)受此启发,请你解下面的方程:
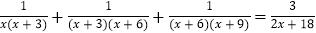 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:a+
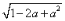 ,其中a=1007.如图是小亮和小芳的解答过程.
,其中a=1007.如图是小亮和小芳的解答过程.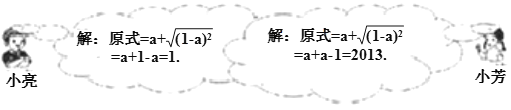
(1)_________的解法是错误的;
(2)错误的原因在于未能正确地运用二次根式的性质:_________;
(3)先化简,再求值:a+2
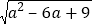 ,其中a=-2007.
,其中a=-2007. -
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)抛物线m1:y1=a1x2+b1x+c1中,函数y1与自变量x之间的部分对应值如表:
设抛物线m1的顶点为P,与y轴的交点为C,则点P的坐标为 , 点C的坐标为 .
(2)将设抛物线m1沿x轴翻折,得到抛物线m2:y2=a2x2+b2x+c2 , 则当x=-3时,y2= .
(3)在(1)的条件下,将抛物线m1沿水平方向平移,得到抛物线m3 . 设抛物线m1与x轴交于A,B两点(点A在点B的左侧),抛物线m3与x轴交于M,N两点(点M在点N的左侧).过点C作平行于x轴的直线,交抛物线m3于点K.问:是否存在以A,C,K,M为顶点的四边形是菱形的情形?若存在,请求出点K的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,要得到△ABD≌△ACE,从下列条件中补选一个,则错误的是( )

A.AB=AC B.DB=EC C.∠ADB=∠AEC D.∠B=∠C
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列要求,解答相关问题.
(1)请补全以下求不等式﹣2x2﹣4x>0的解集的过程.
①构造函数,画出图象:根据不等式特征构造二次函数y=﹣2x2﹣4x;并在下面的坐标系中(图1)画出二次函数y=﹣2x2﹣4x的图象(只画出图象即可).
②求得界点,标示所需,当y=0时,求得方程﹣2x2﹣4x=0的解为( );并用锯齿线标示出函数y=﹣2x2﹣4x图象中y>0的部分.
③借助图象,写出解集:由所标示图象,可得不等式﹣2x2﹣4x>0的解集为﹣2<x<0.请你利用上面求一元一次不等式解集的过程,求不等式x2﹣2x+1≥4的解集.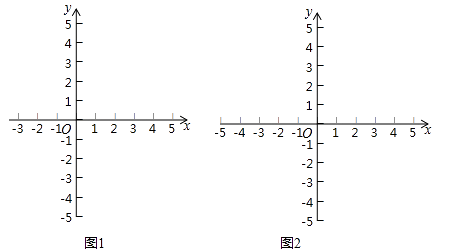
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司以每吨
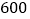 元的价格收购了
元的价格收购了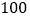 吨某种药材,若直接在市场上销售,每吨的售价是
吨某种药材,若直接在市场上销售,每吨的售价是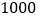 元.该公司决定加工后再出售,相关信息如下表所示:
元.该公司决定加工后再出售,相关信息如下表所示:工艺
每天可加工药材的吨数
成品率
成品售价
(元/吨)
粗加工
14
80%
6000
精加工
6
60%
11000
(注:①成品率80%指加工100吨原料能得到80吨可销售药材;②加工后的废品不产生效益.)
受市场影响,该公司必须在
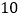 天内将这批药材加工完毕.
天内将这批药材加工完毕.(1)若全部粗加工,可获利_______________________元;
(2)若尽可能多的精加工,剩余的直接在市场上销售,可获利_____________元;
(3)若部分粗加工,部分精加工,恰好
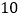 天完成,求可获利多少元?
天完成,求可获利多少元?
相关试题

