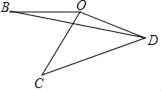
【题目】将线段OB绕点O逆时针旋转60°得到线段OC,继续旋转α(0°<α<120°)得到线段OD,连接CD.
(1)如图,连接BD,则∠BDC的大小=_____(度);
(2)将线段OB放在平面直角坐标系中,O是坐标原点,点B的坐标为(﹣6,0),以OB为斜边作Rt△OBE,使∠OBE=∠OCD,且点E在第三象限,若∠CED=90°,则α的大小=_____(度),点D的坐标为_____.
参考答案:
【答案】 30 90 (3![]() ,﹣3)
,﹣3)
【解析】分析:(1)根据图形旋转的性质可知OB=OC=OD,再由圆周角定理即可得出结论;
(2)如图2,过点O作OM⊥CD于点M,连接EM,先根据AAS定理得出△OEB≌△OMC,故可得出OE=OM,∠BOE=∠COM,所以△OEM是等边三角形.根据OC=OD,OM⊥CD可知CM=DM.故可得出点O、C、D在以M为圆心,MC为半径的圆上.由圆周角定理可得α的大小,再根据三角函数得出结论.
详解:(1)∵线段OC,OD由OB旋转而成,
∴OB=OC=OD.
∴点B、C、D在以O为圆心,AB为半径的圆上.
∴∠BDC=![]() ∠BOC=30°.
∠BOC=30°.
(2)如图2,过点O作OM⊥CD于点M,连接EM,过点D作BF⊥BO的延长线于点F.
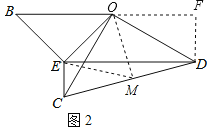
∵∠OMD=90°,
∴∠OMC=90°.
在△OEB与△OMC中,
 ,
,
∴△OEB≌△OMC.
∴OE=OM,∠BOE=∠COM.
∴∠EOM=∠EOC+∠COM=∠EOC+∠BOE=∠BOC=60°.
∴△OEM是等边三角形.
∴EM=OM=OE.
∵OC=OD,OM⊥CD,
∴CM=DM.
又∵∠DEC=90°,
∴EM=CM=DM.
∴OM=CM=DM.
∴点O、C、D、E在以M为圆心,MC为半径的圆上.
∴α=∠COD=90°,
∴∠FOD=30°,
∴OF=3![]() ,DF=3,
,DF=3,
∴点D的坐标为(3![]() ,-3).
,-3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形
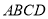 中,
中,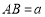 ,
,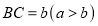 ,将长方形
,将长方形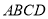 绕点
绕点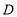 逆时针旋转
逆时针旋转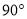 ,点
,点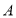 、
、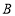 、
、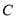 分别对应点
分别对应点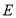 、
、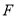 、
、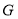 .
.(1)画出长方形
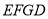 ;
;(2)联结
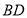 、
、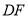 、
、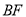 ,请用含有
,请用含有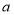 、
、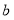 的代数式表示
的代数式表示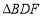 的面积;
的面积;(3)如果
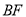 交
交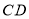 于点
于点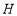 ,请用含有
,请用含有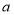 、
、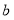 的代数式表示
的代数式表示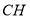 的长度.
的长度.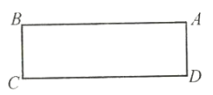
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简、在求值:
(1)(4a2-3a)-(1-4a+4a2),其中a=-2
(2)有8个算式,排成4行2列
2+2,2×2
3+
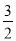 ,3×
,3×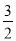
4+
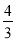 ,4×
,4×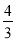
5+
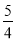 ,5×
,5×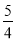
①同一行中两个算式的结果怎样?
②算式2019+
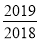 和2019×
和2019×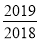 的结果相等吗?
的结果相等吗?③请你写出算式,试一试,再探索其规律,用含自然数n的代数式表示这一规律.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC、BD是菱形ABCD的对角线,那么下列结论一定正确的是( )
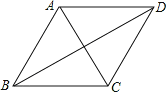
A. △ABD与△ABC的周长相等
B. △ABD与△ABC的面积相等
C. 菱形的周长等于两条对角线之和的两倍
D. 菱形的面积等于两条对角线之积的两倍
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.为提前了解学生的选修情况,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行了整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:

(1)本次调查的学生共有 人,在扇形统计图中,m的值是 ;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请直接写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】江南新校区建设需运送3×105立方米的土石方,闽北运输公司承担了该项工程的运送任务.
(1)写出完成运送任务所需的时间y(单位:天)与公司平均每天的运送量x(单位:立方米/天)之间的关系式是 ;
(2)如果公司平均每天的运送量比原计划提高20%,按这个进度公司可以比规定时间提前10天完成运送任务,那么公司平均每天的运送量x是多少?
(3)实际运送时,公司派出80辆车,每辆车按问题(2)中提高后的运送量运输,若先运送了25天,后来由于工程进度的需要,剩下的任务须在20天内完成,那么公司至少要增加多少辆同样型号的车才能按时完成任务?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E.过点D作DF⊥AC交AC于点F.
(1)求证:DF是⊙O的切线;
(2)若⊙O的半径为8,∠CDF=22.5°,求阴影部分的面积.

相关试题

