【题目】(1)请在横线上填写适当的内容,完成下面的解答过程:
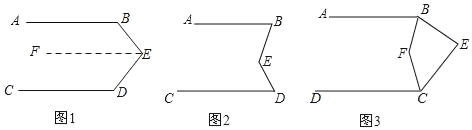
如图①,如果∠ABE+∠BED+∠CDE=360°,试说明AB∥CD.
理由:过点E作EF∥AB
所以∠ABE+∠BEF= °( )
又因为∠ABE+∠BED+∠CDE=360°
所以∠FED+∠CDE= °
所以EF∥ .
又因为EF∥AB,
所以AB∥CD.
(2)如图②,如果AB∥CD,试说明∠BED=∠B+∠D.
(3)如图③,如果AB∥CD,∠BEC=α,BF平分∠ABE,CF平分∠DCE,则∠BFC的度数是 (用含α的代数式表示).
参考答案:
【答案】(1)180,两直线平行,同旁内角互补,180,CD;(2)见解析;(3)180°﹣![]() α.
α.
【解析】
(1)先判断出∠FED+∠CDE=180°得出EF∥CD,即可得出结论;
(2)先判断出∠BEH=∠B,再判断出EH∥CD,得出∠DEH=∠D,即可的得出结论;
(3)先判断出∠ABE+∠DCE=360°-α,进而判断出∠ABF+∠DCF=180°-![]() α,借助(2)的结论即可得出结论.
α,借助(2)的结论即可得出结论.
解:(1)过点E作EF∥AB
∴∠ABE+∠BEF=180°( 两直线平行,同旁内角互补)
∵∠ABE+∠BED+∠CDE=360°
∴∠FED+∠CDE=180°
∴EF∥CD
∵EF∥AB
∴AB∥CD;
故答案为:180,两直线平行,同旁内角互补,180,CD;
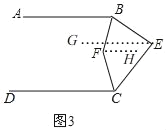
(2)如图2,
过点E作EH∥AB,
∴∠BEH=∠B,
∵EH∥AB,AB∥CD,
∴EH∥CD,
∴∠DEH=∠D,
∴∠BED=∠BEH+∠DEH=∠B+∠D;
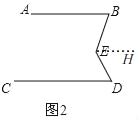
(3)如图3,
过点E作EG∥AB,
∴∠ABE+∠BEG=180°,
∵EG∥AB,CD∥AB,
∴EG∥CD,
∴∠DCE+∠CEG=180°
∴∠ABE+∠BEG+∠CEG+∠DCE=360°,
∴∠ABE+∠BEC+∠DCE=360°,
∴∠ABE+∠DCE=360°﹣∠BEC,
∵∠BEC=α,
∴∠ABE+∠CCE=360°﹣α,
∵BF,CF分别平分∠ABE,∠DCE,
∴∠ABE=2∠ABF,∠DCF=2∠ECF,
∴∠ABF+∠DCF=180°﹣![]() α,
α,
过点F作作FH∥AB,
同(2)的方法得,∠BFC=∠ABF+∠DCF=180°﹣![]() α,
α,
故答案为:180°﹣![]() α.
α.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,新城区新建了三个商业城A,B,C,其中C在A的正东方向,在A处测得B在A的南偏东52°的方向,在C处测得B在C的南偏东26°的方向,已知A和B的距离是1000m.现有甲、乙两个工程对修建道路,甲修建一条从A到C的笔直道路AC,乙修建一条从B到直线AC最近的道路BD.求甲、乙修建的道路各是多长.(结果精确到1m)(参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)

-
科目: 来源: 题型:
查看答案和解析>>【题目】油井A位于油库P南偏东75°方向,主输油管道AP=12km,一新建油井B位于点P的北偏东75°方向,且位于点A的北偏西15°方向.
(1)求∠PBA;
(2)求A,B间的距离;
(3)要在AP上选择一个支管道连接点C,使从点B到点C处的支输油管道最短,求这时BC的长.(结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某社区去年购买了A、B两种型号的共享单车,购买A种单车共花费15000元,购买B种单车共花费14000元,购买A种单车的数量是购买B种单车数量的1.5倍,且购买一辆A种单车比购买一辆B种单车少200元.
(1)求去年购买一辆A种和一辆B种单车各需要多少元?
(2)为积极响应政府提出的“绿色发展低碳出行”号召,该社区决定今年再买A、B两种型号的单车共60辆,恰逢厂家对A、B两种型号单车的售价进行调整,A种单车售价比去年购买时提高了10%,B种单车售价比去年购买时降低了10%,如果今年购买A、B两种单车的总费用不超过34000元,那么该社区今年最多购买多少辆B种单车?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC是矩形ABCD的对角线,AC的垂直平分线EF分别交BC、AD于点E和F,EF交AC于点O.
(1)求证:四边形AECF是菱形;(2)若AB=6,AD=8,求四边形AECF的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点P表示广场上的一盏照明灯.
(1)请你在图中画出小敏在照明灯P照射下的影子(用线段表示);
(2)若小丽到灯柱MO的距离为4.5米,照明灯P到灯柱的距离为1.5米,小丽目测照明灯P的仰角为55°,她的目高QB为1.6米,试求照明灯P到地面的距离(结果精确到0.1米).
(参考数据:tan55°≈1.428,sin55°≈0.819,cos55°≈0.574)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=
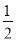 x+2与x轴交于点A,与y轴交于点C,抛物线y=
x+2与x轴交于点A,与y轴交于点C,抛物线y=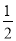 x2+bx+c经过A、C两点,与x轴的另一交点为点B.
x2+bx+c经过A、C两点,与x轴的另一交点为点B.
(1)求抛物线的函数表达式;
(2)点D为直线AC上方抛物线上一动点;
①连接BC、CD,设直线BD交线段AC于点E,△CDE的面积为S1, △BCE的面积为S2, 求
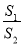 的最大值;
的最大值;②过点D作DF⊥AC,垂足为点F,连接CD,是否存在点D,使得△CDF中的某个角恰好等于∠BAC的2倍?若存在,求点D的横坐标;若不存在,请说明理由
相关试题

