【题目】如图,在平面直角坐标系中,直线y=![]() x+2与x轴交于点A,与y轴交于点C,抛物线y=
x+2与x轴交于点A,与y轴交于点C,抛物线y=![]() x2+bx+c经过A、C两点,与x轴的另一交点为点B.
x2+bx+c经过A、C两点,与x轴的另一交点为点B.

(1)求抛物线的函数表达式;
(2)点D为直线AC上方抛物线上一动点;
①连接BC、CD,设直线BD交线段AC于点E,△CDE的面积为S1, △BCE的面积为S2, 求![]() 的最大值;
的最大值;
②过点D作DF⊥AC,垂足为点F,连接CD,是否存在点D,使得△CDF中的某个角恰好等于∠BAC的2倍?若存在,求点D的横坐标;若不存在,请说明理由
参考答案:
【答案】(1)![]() (2)①当a=2时,
(2)①当a=2时, ![]() 的最大值是
的最大值是![]() ②﹣2或﹣
②﹣2或﹣![]()
【解析】试题分析:(1)根据题意得到A(﹣4,0),C(0,2)代入y=﹣![]() x2+bx+c,于是得到结论;(2)①如图,令y=0,解方程得到x1=﹣4,x2=1,求得B(1,0),过D作DM⊥x轴于M,过B作BN⊥x轴交于AC于N,根据相似三角形的性质即可得到结论;②根据勾股定理的逆定理得到△ABC是以∠ACB为直角的直角三角形,取AB的中点P,求得P(﹣
x2+bx+c,于是得到结论;(2)①如图,令y=0,解方程得到x1=﹣4,x2=1,求得B(1,0),过D作DM⊥x轴于M,过B作BN⊥x轴交于AC于N,根据相似三角形的性质即可得到结论;②根据勾股定理的逆定理得到△ABC是以∠ACB为直角的直角三角形,取AB的中点P,求得P(﹣![]() ,0),得到PA=PC=PB=
,0),得到PA=PC=PB=![]() ,过作x轴的平行线交y轴于R,交AC的延线于G,情况一:如图,∠DCF=2∠BAC=∠DGC+∠CDG,情况二,∠FDC=2∠BAC,解直角三角形即可得到结论.
,过作x轴的平行线交y轴于R,交AC的延线于G,情况一:如图,∠DCF=2∠BAC=∠DGC+∠CDG,情况二,∠FDC=2∠BAC,解直角三角形即可得到结论.
试题解析:(1)解:根据题意得A(﹣4,0),C(0,2),
∵抛物线y=﹣ ![]() x2+bx+c经过A、C两点,
x2+bx+c经过A、C两点,
∴ ![]() ,
,
∴ ![]() ,
,
∴y=﹣ ![]() x2﹣
x2﹣ ![]() x+2
x+2
(2)解:①如图,
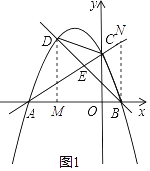
令y=0,
∴﹣ ![]() x2﹣
x2﹣ ![]() x+2=0,
x+2=0,
∴x1=﹣4,x2=1,
∴B(1,0),
过D作DM⊥x轴于M,过B作BN⊥x轴交于AC于N,
∴DM∥BN,
∴△DME∽△BNE,
∴ ![]() =
= ![]() =
= ![]() ,
,
设D(a,=﹣ ![]() a2﹣
a2﹣ ![]() a+2),
a+2),
∴M(a, ![]() a+2),
a+2),
∵B(1.0),
∴N(1, ![]() ),
),
∴ ![]() =
= ![]() =
= ![]() (a+2)2+
(a+2)2+ ![]() ;
;
∴当a=2时, ![]() 的最大值是
的最大值是 ![]() ;
;
②∵A(﹣4,0),B(1,0),C(0,2),
∴AC=2 ![]() ,BC=
,BC= ![]() ,AB=5,
,AB=5,
∴AC2+BC2=AB2 ,
∴△ABC是以∠ACB为直角的直角三角形,取AB的中点P,
∴P(﹣ ![]() ,0),
,0),
∴PA=PC=PB= ![]() ,
,
∴∠CPO=2∠BAC,
∴tan∠CPO=tan(2∠BAC)= ![]() ,
,
过作x轴的平行线交y轴于R,交AC的延长线于G,
情况一:如图,
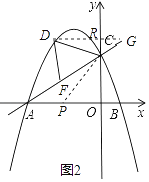
∴∠DCF=2∠BAC=∠DGC+∠CDG,
∴∠CDG=∠BAC,
∴tan∠CDG=tan∠BAC= ![]() ,
,
即 ![]() ,
,
令D(a,﹣ ![]() a2﹣
a2﹣ ![]() a+2),
a+2),
∴DR=﹣a,RC=﹣ ![]() a2﹣
a2﹣ ![]() a,
a,
∴ ![]() ,
,
∴a1=0(舍去),a2=﹣2,
∴xD=﹣2,
情况二,∴∠FDC=2∠BAC,
∴tan∠FDC= ![]() ,
,
设FC=4k,
∴DF=3k,DC=5k,
∵tan∠DGC= ![]() =
= ![]() ,
,
∴FG=6k,
∴CG=2k,DG=3 ![]() k,∴
k,∴
∴RC= ![]() k,RG=
k,RG= ![]() k,
k,
DR=3 ![]() k﹣
k﹣ ![]() k=
k= ![]() k,
k,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴a1=0(舍去),a2= ![]() ,
,
点D的横坐标为﹣2或﹣ ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)请在横线上填写适当的内容,完成下面的解答过程:
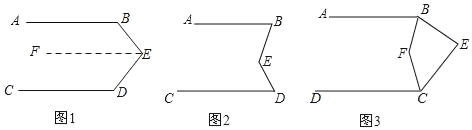
如图①,如果∠ABE+∠BED+∠CDE=360°,试说明AB∥CD.
理由:过点E作EF∥AB
所以∠ABE+∠BEF= °( )
又因为∠ABE+∠BED+∠CDE=360°
所以∠FED+∠CDE= °
所以EF∥ .
又因为EF∥AB,
所以AB∥CD.
(2)如图②,如果AB∥CD,试说明∠BED=∠B+∠D.
(3)如图③,如果AB∥CD,∠BEC=α,BF平分∠ABE,CF平分∠DCE,则∠BFC的度数是 (用含α的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC是矩形ABCD的对角线,AC的垂直平分线EF分别交BC、AD于点E和F,EF交AC于点O.
(1)求证:四边形AECF是菱形;(2)若AB=6,AD=8,求四边形AECF的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点P表示广场上的一盏照明灯.
(1)请你在图中画出小敏在照明灯P照射下的影子(用线段表示);
(2)若小丽到灯柱MO的距离为4.5米,照明灯P到灯柱的距离为1.5米,小丽目测照明灯P的仰角为55°,她的目高QB为1.6米,试求照明灯P到地面的距离(结果精确到0.1米).
(参考数据:tan55°≈1.428,sin55°≈0.819,cos55°≈0.574)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=
 .其中正确的结论有( )
.其中正确的结论有( )
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,直线y1=2x﹣2与坐标轴交于A,B两点,与双曲线y2=
 (x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:①当x>0时,y1随x的增大而增大,y2随x的增大而减小;②
(x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:①当x>0时,y1随x的增大而增大,y2随x的增大而减小;② ;③当0<x<2时,y1<y2;④如图,当x=4时,EF=4.其中正确结论的个数是( )
;③当0<x<2时,y1<y2;④如图,当x=4时,EF=4.其中正确结论的个数是( )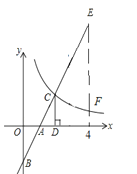
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】初二年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初二学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:

(1)在这次评价中,一共抽查了 名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为 度;
(3)请将频数分布直方图补充完整;
(4)如果全市有6000名初二学生,那么在试卷评讲课中,“独立思考”的初二学生约有多少人?
相关试题

