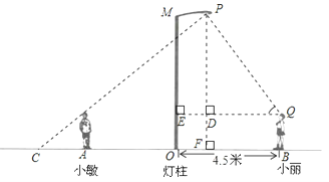
【题目】如图所示,点P表示广场上的一盏照明灯.
(1)请你在图中画出小敏在照明灯P照射下的影子(用线段表示);
(2)若小丽到灯柱MO的距离为4.5米,照明灯P到灯柱的距离为1.5米,小丽目测照明灯P的仰角为55°,她的目高QB为1.6米,试求照明灯P到地面的距离(结果精确到0.1米).
(参考数据:tan55°≈1.428,sin55°≈0.819,cos55°≈0.574)

参考答案:
【答案】(1)线段AC是小敏的影子(2)照明灯到地面的距离为5.9米
【解析】试题分析:(1)第一问作图相对简单,直接连接P点和小敏头顶,延长线和地面交点C和A的连线即为影子;
(2)第二问.过点Q作QE⊥MO于E,过点P作PF⊥AB于F,交EQ于点D,要求P到地面的距离,由题可知,只需求出PD即可,而在三角形PDQ中,55°角的邻边数值已知,求对边,可用正切便可求出PD=3tan55°≈4.3(米),再加上眼睛高度1.6,便可求出照明灯到地面的距离为5.9米.
试题解析:(1)如图线段AC是小敏的影子;
(2)过点Q作QE⊥MO于E,
过点P作PF⊥AB于F,交EQ于点D,
则PF⊥EQ,
在Rt△PDQ中,∠PQD=55°,
DQ=EQ﹣ED
=4.5﹣1.5
=3(米),
∵tan55°=![]() ,
,
∴PD=3tan55°≈4.3(米),
∵DF=QB=1.6米,
∴PF=PD+DF=4.3+1.6=5.9(米)
答:照明灯到地面的距离为5.9米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某社区去年购买了A、B两种型号的共享单车,购买A种单车共花费15000元,购买B种单车共花费14000元,购买A种单车的数量是购买B种单车数量的1.5倍,且购买一辆A种单车比购买一辆B种单车少200元.
(1)求去年购买一辆A种和一辆B种单车各需要多少元?
(2)为积极响应政府提出的“绿色发展低碳出行”号召,该社区决定今年再买A、B两种型号的单车共60辆,恰逢厂家对A、B两种型号单车的售价进行调整,A种单车售价比去年购买时提高了10%,B种单车售价比去年购买时降低了10%,如果今年购买A、B两种单车的总费用不超过34000元,那么该社区今年最多购买多少辆B种单车?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)请在横线上填写适当的内容,完成下面的解答过程:
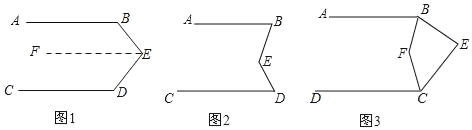
如图①,如果∠ABE+∠BED+∠CDE=360°,试说明AB∥CD.
理由:过点E作EF∥AB
所以∠ABE+∠BEF= °( )
又因为∠ABE+∠BED+∠CDE=360°
所以∠FED+∠CDE= °
所以EF∥ .
又因为EF∥AB,
所以AB∥CD.
(2)如图②,如果AB∥CD,试说明∠BED=∠B+∠D.
(3)如图③,如果AB∥CD,∠BEC=α,BF平分∠ABE,CF平分∠DCE,则∠BFC的度数是 (用含α的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC是矩形ABCD的对角线,AC的垂直平分线EF分别交BC、AD于点E和F,EF交AC于点O.
(1)求证:四边形AECF是菱形;(2)若AB=6,AD=8,求四边形AECF的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=
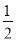 x+2与x轴交于点A,与y轴交于点C,抛物线y=
x+2与x轴交于点A,与y轴交于点C,抛物线y=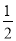 x2+bx+c经过A、C两点,与x轴的另一交点为点B.
x2+bx+c经过A、C两点,与x轴的另一交点为点B.
(1)求抛物线的函数表达式;
(2)点D为直线AC上方抛物线上一动点;
①连接BC、CD,设直线BD交线段AC于点E,△CDE的面积为S1, △BCE的面积为S2, 求
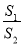 的最大值;
的最大值;②过点D作DF⊥AC,垂足为点F,连接CD,是否存在点D,使得△CDF中的某个角恰好等于∠BAC的2倍?若存在,求点D的横坐标;若不存在,请说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=
 .其中正确的结论有( )
.其中正确的结论有( )
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,直线y1=2x﹣2与坐标轴交于A,B两点,与双曲线y2=
 (x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:①当x>0时,y1随x的增大而增大,y2随x的增大而减小;②
(x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:①当x>0时,y1随x的增大而增大,y2随x的增大而减小;② ;③当0<x<2时,y1<y2;④如图,当x=4时,EF=4.其中正确结论的个数是( )
;③当0<x<2时,y1<y2;④如图,当x=4时,EF=4.其中正确结论的个数是( )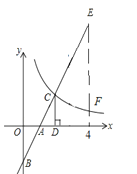
A. 1 B. 2 C. 3 D. 4
相关试题

