【题目】如图,点A(1,2)在反比例函数y= ![]() (x>0)上,B为反比例函数图象上一点,不与A重合,当以OB为直径的圆经过A点,点B的坐标为( )
(x>0)上,B为反比例函数图象上一点,不与A重合,当以OB为直径的圆经过A点,点B的坐标为( )
A.(2,1)
B.(3, ![]() )
)
C.(4,0.5)
D.(5,0.4)
参考答案:
【答案】C
【解析】解:将点A(1,2)代入y= ![]() ,得:k=2,
,得:k=2,
则反比例函数解析式为y= ![]() ,
,
设点B(m, ![]() ),
),
如图,连接AB,过点A作x轴的平行线,交y轴于点C,过点B作y轴的平行线,交直线AC于点D,
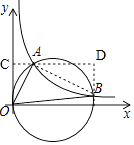
则∠OCA=∠D=90°,
∴∠AOC+∠OAC=90°,
∵OB为圆的直径,
∴∠OAB=90°,
∴∠OAC+∠BAD=90°,
∴∠AOC=∠BAD,
则△AOC∽△BAD,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得:m=1(舍)或m=4,
则点B(4,0.5),
故C符合题意.
所以答案是:C.
【考点精析】通过灵活运用圆周角定理,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
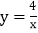 和
和 在第一象限内的图象如图所示,点
在第一象限内的图象如图所示,点 是
是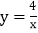 的图象上一动点,作
的图象上一动点,作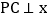 轴于点
轴于点 ,交
,交 的图象于点
的图象于点 ,作
,作 轴于点
轴于点 ,交
,交 的图象于点
的图象于点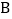 ,给出如下结论:①
,给出如下结论:①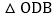 与
与 的面积相等;②
的面积相等;②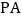 与
与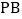 始终相等;③四边形
始终相等;③四边形 的面积大小不会发生变化;④
的面积大小不会发生变化;④ ,其中正确的结论序号是( )
,其中正确的结论序号是( )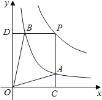
A. ①②③ B. ②③④ C. ①③④ D. ①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上三点M,O,N对应的数分别为﹣1,0,3,点P为数轴上任意点,其对应的数为x.

(1)MN的长为 ;
(2)如果点P到点M、点N的距离相等,那么x的值是: ;
(3)如果点P以每分钟2个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
, ,
, 是
是 边上一点,延长
边上一点,延长 到点
到点 ,使得
,使得 ,连接
,连接 ,过点
,过点 作
作 的垂线,交
的垂线,交 的垂直平分线于点
的垂直平分线于点 ,连接
,连接 .
.(1)如图1,当点
 与点
与点 重合时,证明:
重合时,证明: ;
;
(2)如图2,当点
 不与
不与 ,
, 两点重合时,(1)中的结论是否还成立?并说明理由.
两点重合时,(1)中的结论是否还成立?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A在O正北方向,B在O正东方向,且A、B到点O的距离相等,甲从A出发,以每小时60千米的速度朝正东方向行驶,乙从B出发,以每小时40千米的速度朝正北方向行驶,1小时后,位于点O处的观察员发现甲乙两人之间的夹角为45°,此时甲乙两人相距( )千米。

A. 80 B. 50
 C. 100
C. 100 D. 100
D. 100 -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列两个等式:
 ,
,  ,给出定义如下:
,给出定义如下:我们称使等式
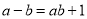 成立的一对有理数
成立的一对有理数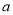 ,
,  为“共生有理数对”,记为(
为“共生有理数对”,记为(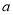 ,
, 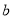 ),如:数对(
),如:数对(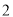 ,
,  ),(
),(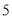 ,
,  ),都是“共生有理数对”.
),都是“共生有理数对”.(1)判断数对(
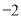 ,
, 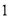 ),(
),( ,
, 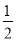 )是不是“共生有理数对”,写出过程;
)是不是“共生有理数对”,写出过程;(2)若(
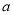 ,
,  )是“共生有理数对”,求
)是“共生有理数对”,求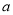 的值;
的值;(3)若(
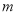 ,
, 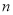 )是“共生有理数对”,则(
)是“共生有理数对”,则(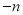 ,
, 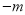 ) “共生有理数对”(填“是”或“不是”);说明理由;
) “共生有理数对”(填“是”或“不是”);说明理由;(4)请再写出一对符合条件的 “共生有理数对”为 (注意:不能与题目中已有的“共生有理数对”重复)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BC=2,A为半径为1的⊙B上一点,连接AC,在AC上方作一个正六边形ACDEFG,连接BD,则BD的最大值为 .

相关试题

