【题目】已知![]() ,
,![]() ,
,![]() 是
是![]() 边上一点,延长
边上一点,延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 的垂直平分线于点
的垂直平分线于点![]() ,连接
,连接![]() .
.
(1)如图1,当点![]() 与点
与点![]() 重合时,证明:
重合时,证明:![]() ;
;

(2)如图2,当点![]() 不与
不与![]() ,
,![]() 两点重合时,(1)中的结论是否还成立?并说明理由.
两点重合时,(1)中的结论是否还成立?并说明理由.
参考答案:
【答案】(1)见解析(2)成立,理由见解析
【解析】
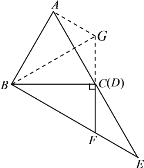
(1)延长FD至点G,使得DG=DF,连接BG,AG.
先证明△ADG≌△EDF,得到AG=EF.再证明△ABG≌△DBF,得到∠ABG=∠DBF,即有∠ABG=∠DBG=![]() ∠ABC=30°,进而得到∠DBF=30°,根据30°角所对的直角边等于斜边的一半即可得到结论.
∠ABC=30°,进而得到∠DBF=30°,根据30°角所对的直角边等于斜边的一半即可得到结论.
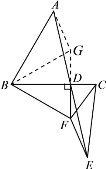
(2)成立.延长FD至点![]() ,使得DG=DF,连接BG,AG.
,使得DG=DF,连接BG,AG.
通过证明△ADG≌△EDF,得到AG=EF.由垂直平分线的性质得到FC=FE,从而有AG=CF.
即可得到△ABG≌△CBF,由全等三角形对应角相等得到∠ABG=∠CBF,即有∠ABG=∠GBD.进而得出∠DBF=∠GBD=30°,根据30°角所对的直角边等于斜边的一半即可得到结论.
延长FD至点G,使得DG=DF,连接BG,AG.
∵DF⊥BC于点![]() ,∴∠BDF=90°,∴BG=BF,∴∠DBF=∠DBG.
,∴∠BDF=90°,∴BG=BF,∴∠DBF=∠DBG.
又∵AD=ED,∠ADG=∠EDF,DG=DF,∴△ADG≌△EDF(SAS),∴AG=EF.
∵点![]() 在CE的垂直平分线上,点
在CE的垂直平分线上,点![]() 与点
与点![]() 重合,∴DF=EF,∴DF=AG.
重合,∴DF=EF,∴DF=AG.
∵AB=BC,∴△ABG≌△DBF(SSS),∴∠ABG=∠DBF,∴∠ABG=∠DBG=![]() ∠ABC=30°,∴∠DBF=30°,∴BG=2DG,∴BF=2DF.
∠ABC=30°,∴∠DBF=30°,∴BG=2DG,∴BF=2DF.
(2)成立.理由如下:
延长FD至点![]() ,使得DG=DF,连接BG,AG.
,使得DG=DF,连接BG,AG.
∵DF⊥BC于点![]() ,∴∠BDF=90°,∴BG=BF,∴∠DBF=∠DBG.
,∴∠BDF=90°,∴BG=BF,∴∠DBF=∠DBG.
又∵AD=ED,∠ADG=∠EDF,∴△ADG≌△EDF(SAS),∴AG=EF.
∵点![]() 在CE的垂直平分线上,∴FC=FE,∴AG=CF.
在CE的垂直平分线上,∴FC=FE,∴AG=CF.
又∵AB=BC,∴△ABG≌△CBF(SSS),∴∠ABG=∠CBF,∴∠ABG=∠GBD.
又∵∠ABC=60°,∴∠GBD=30°,∴∠DBF=∠GBD=30°,∴BF=2DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
 ,
, .
.(1)当
 >0时,判断
>0时,判断 与0的关系,并说明理由;
与0的关系,并说明理由;(2)设
 .
.①当
 时,求
时,求 的值;
的值;②若
 是整数,求
是整数,求 的正整数值.
的正整数值. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数
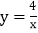 和
和 在第一象限内的图象如图所示,点
在第一象限内的图象如图所示,点 是
是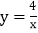 的图象上一动点,作
的图象上一动点,作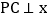 轴于点
轴于点 ,交
,交 的图象于点
的图象于点 ,作
,作 轴于点
轴于点 ,交
,交 的图象于点
的图象于点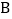 ,给出如下结论:①
,给出如下结论:①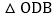 与
与 的面积相等;②
的面积相等;②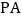 与
与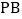 始终相等;③四边形
始终相等;③四边形 的面积大小不会发生变化;④
的面积大小不会发生变化;④ ,其中正确的结论序号是( )
,其中正确的结论序号是( )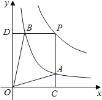
A. ①②③ B. ②③④ C. ①③④ D. ①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上三点M,O,N对应的数分别为﹣1,0,3,点P为数轴上任意点,其对应的数为x.

(1)MN的长为 ;
(2)如果点P到点M、点N的距离相等,那么x的值是: ;
(3)如果点P以每分钟2个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(1,2)在反比例函数y=
 (x>0)上,B为反比例函数图象上一点,不与A重合,当以OB为直径的圆经过A点,点B的坐标为( )
(x>0)上,B为反比例函数图象上一点,不与A重合,当以OB为直径的圆经过A点,点B的坐标为( )
A.(2,1)
B.(3, )
)
C.(4,0.5)
D.(5,0.4) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A在O正北方向,B在O正东方向,且A、B到点O的距离相等,甲从A出发,以每小时60千米的速度朝正东方向行驶,乙从B出发,以每小时40千米的速度朝正北方向行驶,1小时后,位于点O处的观察员发现甲乙两人之间的夹角为45°,此时甲乙两人相距( )千米。

A. 80 B. 50
 C. 100
C. 100 D. 100
D. 100 -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列两个等式:
 ,
,  ,给出定义如下:
,给出定义如下:我们称使等式
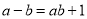 成立的一对有理数
成立的一对有理数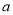 ,
,  为“共生有理数对”,记为(
为“共生有理数对”,记为(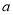 ,
, 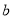 ),如:数对(
),如:数对(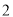 ,
,  ),(
),(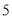 ,
,  ),都是“共生有理数对”.
),都是“共生有理数对”.(1)判断数对(
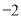 ,
, 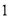 ),(
),( ,
, 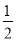 )是不是“共生有理数对”,写出过程;
)是不是“共生有理数对”,写出过程;(2)若(
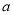 ,
,  )是“共生有理数对”,求
)是“共生有理数对”,求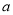 的值;
的值;(3)若(
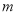 ,
, 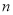 )是“共生有理数对”,则(
)是“共生有理数对”,则(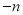 ,
, 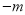 ) “共生有理数对”(填“是”或“不是”);说明理由;
) “共生有理数对”(填“是”或“不是”);说明理由;(4)请再写出一对符合条件的 “共生有理数对”为 (注意:不能与题目中已有的“共生有理数对”重复)
相关试题

