【题目】观察下列两个等式: ![]() ,
, ![]() ,给出定义如下:
,给出定义如下:
我们称使等式![]() 成立的一对有理数
成立的一对有理数![]() ,
, ![]() 为“共生有理数对”,记为(
为“共生有理数对”,记为(![]() ,
, ![]() ),如:数对(
),如:数对(![]() ,
, ![]() ),(
),(![]() ,
, ![]() ),都是“共生有理数对”.
),都是“共生有理数对”.
(1)判断数对(![]() ,
, ![]() ),(
),(![]() ,
, ![]() )是不是“共生有理数对”,写出过程;
)是不是“共生有理数对”,写出过程;
(2)若(![]() ,
, ![]() )是“共生有理数对”,求
)是“共生有理数对”,求![]() 的值;
的值;
(3)若(![]() ,
, ![]() )是“共生有理数对”,则(
)是“共生有理数对”,则(![]() ,
, ![]() ) “共生有理数对”(填“是”或“不是”);说明理由;
) “共生有理数对”(填“是”或“不是”);说明理由;
(4)请再写出一对符合条件的 “共生有理数对”为 (注意:不能与题目中已有的“共生有理数对”重复)
参考答案:
【答案】(1)(![]() ,
, ![]() );(2)
);(2)![]() (3)是(4)(
(3)是(4)(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() )
)
【解析】试题分析:(1)利用共生有理数对的定义即可判断;
(2)把a,3带入![]() 中,得到关于a的一元一次方程,解得a值即可;
中,得到关于a的一元一次方程,解得a值即可;
(3)依据定义判断即可;
(4)依据定义写出一对数值即可,注意答案不唯一.
试题解析:(1)-2-1=-3,(-2) ×1+1=-1,-3≠-1,故(![]() ,
, ![]() )不是共生有理数对;
)不是共生有理数对;
3-![]() =
=![]() ,3×
,3×![]() +1=
+1=![]() ,故(3,
,故(3, ![]() )是共生有理数对;
)是共生有理数对;
(2)由题意得: ![]() ,解得
,解得![]() .
.
(3)是.
理由: ![]() ,
, ![]() ,
,
∵(m,n)是“共生有理数对”
∴m-n=mn+1,
∴-n+m=mn+1,
∴(-n,-m)是“共生有理数对”;
(4)(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() )等(答案不唯一,只要不和题中重复即可).
)等(答案不唯一,只要不和题中重复即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
, ,
, 是
是 边上一点,延长
边上一点,延长 到点
到点 ,使得
,使得 ,连接
,连接 ,过点
,过点 作
作 的垂线,交
的垂线,交 的垂直平分线于点
的垂直平分线于点 ,连接
,连接 .
.(1)如图1,当点
 与点
与点 重合时,证明:
重合时,证明: ;
;
(2)如图2,当点
 不与
不与 ,
, 两点重合时,(1)中的结论是否还成立?并说明理由.
两点重合时,(1)中的结论是否还成立?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(1,2)在反比例函数y=
 (x>0)上,B为反比例函数图象上一点,不与A重合,当以OB为直径的圆经过A点,点B的坐标为( )
(x>0)上,B为反比例函数图象上一点,不与A重合,当以OB为直径的圆经过A点,点B的坐标为( )
A.(2,1)
B.(3, )
)
C.(4,0.5)
D.(5,0.4) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A在O正北方向,B在O正东方向,且A、B到点O的距离相等,甲从A出发,以每小时60千米的速度朝正东方向行驶,乙从B出发,以每小时40千米的速度朝正北方向行驶,1小时后,位于点O处的观察员发现甲乙两人之间的夹角为45°,此时甲乙两人相距( )千米。

A. 80 B. 50
 C. 100
C. 100 D. 100
D. 100 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BC=2,A为半径为1的⊙B上一点,连接AC,在AC上方作一个正六边形ACDEFG,连接BD,则BD的最大值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】A,B两地被大山阻隔,若要从A地到B地,只能沿着如图所示的公路先从A地到C地,再由C地到B地.现计划开凿隧道A,B两地直线贯通,经测量得:∠CAB=30°,∠CBA=45°,AC=20km,求隧道开通后与隧道开通前相比,从A地到B地的路程将缩短多少?(结果精确到0.1km,参考数据:
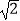 ≈1.414,
≈1.414, 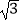 ≈1.732)
≈1.732)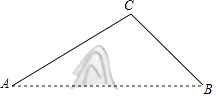
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,有一个面积为1的正方形,经过一次“生长”后,在它的左右肩上生出两个小正方形,如图2,其中,三个正方形围成的三角形是直角三角形.再经过一次“生长”后,变成图3;“生长”10次后,如果继续“生长”下去,它将变得更加“枝繁叶茂”.
随着不断地“生长”,形成的图形中所有正方形的面积和也随之变化.若生长n次后,变成的图中所有正方形的面积用Sn表示,求回答:
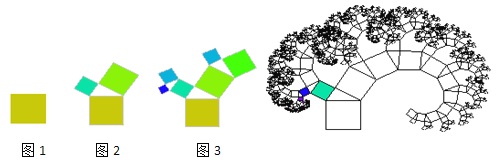
(1)S0= ,S1= ,S2= ,S3= ;
(2)S0+S1+S2+…+S10= .
相关试题

