【题目】如图,在△ABC中,AD,BE分别是BC,AC边上的高.求证:△DCE∽△ACB. 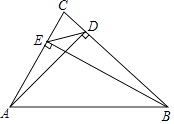
参考答案:
【答案】证明:∵在△ABC中,AD、BE分别是BC、AC边上的高,
∴∠ADC=∠BEC=90°,
∵∠C是公共角,
∴△CDE∽△CAB,
∴CD:CE=CA:CB,
∴CD:CA=CE:CB,
∴△DCE∽△ACB
【解析】首先由在△ABC中,AD、BE分别是BC、AC边上的高,证得△CDE∽△CAB,即可得CD:CA=CE:CB,继而证得结论.
【考点精析】利用相似三角形的判定对题目进行判断即可得到答案,需要熟知相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣22×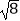 +|1﹣
+|1﹣ 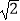 |+6sin45°+1
|+6sin45°+1
(2)3tan30°﹣2tan45°+2sin60°+4cos60°. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,AD与BE相交于点F,且AE=CD.
(1)求证:AD=BE;
(2)求∠BFD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=135°,AB=20,AC=30,求△ABC的面积.
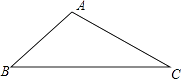
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=AC,直线MN经过点A,过点B作BD⊥MN于D,过C作CE⊥MN于E.
(1)求证:△ABD≌△CAE;
(2)若BD=12cm,DE=20cm,求CE的长度.
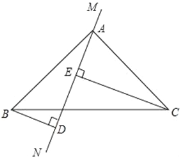
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(﹣3,0),与反比例函数y=
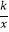 在第一象限的图象交于点B(3,m),连接BO,若△AOB面积为9,
在第一象限的图象交于点B(3,m),连接BO,若△AOB面积为9, 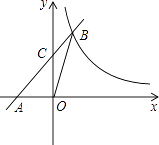
(1)求反比例函数的表达式和直线AB的表达式;
(2)若直线AB与y轴交于点C,求△COB的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果ax+b=0,其中a、b为有理数,x为无理数,那么a=0且b=0.
运用上述知识,解决下列问题:
(1)如果(a-2)
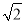 +b+3=0,其中a、b为有理数,那么a= ,b= ;
+b+3=0,其中a、b为有理数,那么a= ,b= ;(2)如果(2+
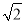 )a-(1-
)a-(1-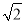 )b=5,其中a、b为有理数,求a+2b的值.
)b=5,其中a、b为有理数,求a+2b的值.
相关试题

