【题目】如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(﹣3,0),与反比例函数y= ![]() 在第一象限的图象交于点B(3,m),连接BO,若△AOB面积为9,
在第一象限的图象交于点B(3,m),连接BO,若△AOB面积为9, 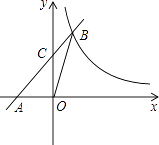
(1)求反比例函数的表达式和直线AB的表达式;
(2)若直线AB与y轴交于点C,求△COB的面积.
参考答案:
【答案】
(1)解:∵A点的坐标为(﹣3,0),
∴OA=3,
又∵点B(3,m)在第一象限,且△AOB面积为9,
∴ ![]() OAm═9,即
OAm═9,即 ![]() ×3m=9,解得m=6,
×3m=9,解得m=6,
∴点B的坐标为(3,6),
将B(3,6)代入y= ![]() 中,得6=
中,得6= ![]() ,则k=18,
,则k=18,
∴反比例函数为:y= ![]() ,
,
设直线AB的表达式为y=ax+b,则 ![]()
解得 ![]()
∴直线AB的表达式为y=x+3
(2)解:在y=x+3中,令x=0,得y=3,
∴点C的坐标为 (0,3),
∴OC=3,
则△COB的面积为: ![]() OC×3=
OC×3= ![]() ×3×3=
×3×3= ![]()
【解析】(1)利用△AOB面积为9,求出m的值,即可求出反比例函数解析式,再利用A,B的坐标求出一次函数式.(2)先求出OC,再利用△COB的面积为= ![]() OC×3,求出△COB的面积.
OC×3,求出△COB的面积.
-
科目: 来源: 题型:
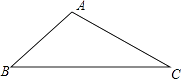
查看答案和解析>>【题目】如图,在△ABC中,∠A=135°,AB=20,AC=30,求△ABC的面积.
-
科目: 来源: 题型:
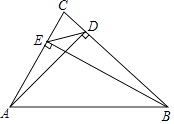
查看答案和解析>>【题目】如图,在△ABC中,AD,BE分别是BC,AC边上的高.求证:△DCE∽△ACB.
-
科目: 来源: 题型:
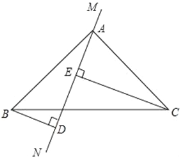
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=AC,直线MN经过点A,过点B作BD⊥MN于D,过C作CE⊥MN于E.
(1)求证:△ABD≌△CAE;
(2)若BD=12cm,DE=20cm,求CE的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果ax+b=0,其中a、b为有理数,x为无理数,那么a=0且b=0.
运用上述知识,解决下列问题:
(1)如果(a-2)
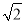 +b+3=0,其中a、b为有理数,那么a= ,b= ;
+b+3=0,其中a、b为有理数,那么a= ,b= ;(2)如果(2+
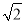 )a-(1-
)a-(1-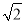 )b=5,其中a、b为有理数,求a+2b的值.
)b=5,其中a、b为有理数,求a+2b的值. -
科目: 来源: 题型:
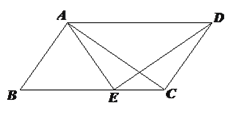
查看答案和解析>>【题目】如图,在四边形ABCD中,AB//CD,∠B=∠ADC,点E是BC边上的一点,且AE=DC.
(1)求证:△ABC≌△EAD ;
(2)如果AB⊥AC,求证:∠BAE= 2∠ACB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ACD和△BCE中,AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,AD与BE相交于点P,则∠BPD的度数为( )
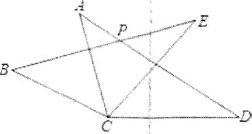
A. 120° B. 125° C. 130° D. 155°
相关试题

