【题目】如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,AD与BE相交于点F,且AE=CD.
(1)求证:AD=BE;
(2)求∠BFD的度数.

参考答案:
【答案】(1)见解析;(2)60°.
【解析】
(1)利用等边三角形的性质得到一对边相等,一对角相等,再根据已知边相等,利用SAS得到三角形全等,利用全等三角形的对应边相等即可得证;
(2)利用全等三角形对应角相等得到一对角相等,再利用外角性质及等边三角形的性质求出所求角度数.
证明:如图,△ABC为等边三角形,
∴AB=AC, ∠BAC=∠C=60°,
在△ABE和△CAD中,
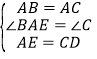 ,
,
∴△ABE≌△CAD,
∴AD=BE,
(2)由(1)得△ABE≌△CAD,
∴∠ABE=∠CAD,
又∠BFD是△ABF的外角,
∴∠BFD=∠BAD+∠ABE=∠BAD+∠CAD,
又∠BAC=∠BAD+∠CAD=60°,
∴∠BFD=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,当太阳在A处时,小明测得某树的影长为2米,当太阳在B处时又测得该树的影长为8米.若两次日照的光线互相垂直,则这棵树的高度为米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰△ABC中,AB=AC,BC∥x轴,点A,C在反比例函数y=
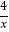 (x>0)的图象上,点B在反比例函数y=
(x>0)的图象上,点B在反比例函数y= 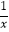 (x>0)的图象上,则△ABC的面积为 .
(x>0)的图象上,则△ABC的面积为 . 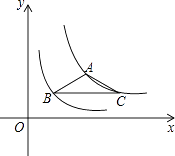
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣22×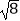 +|1﹣
+|1﹣ 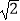 |+6sin45°+1
|+6sin45°+1
(2)3tan30°﹣2tan45°+2sin60°+4cos60°. -
科目: 来源: 题型:
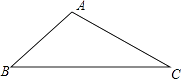
查看答案和解析>>【题目】如图,在△ABC中,∠A=135°,AB=20,AC=30,求△ABC的面积.
-
科目: 来源: 题型:
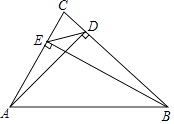
查看答案和解析>>【题目】如图,在△ABC中,AD,BE分别是BC,AC边上的高.求证:△DCE∽△ACB.
-
科目: 来源: 题型:
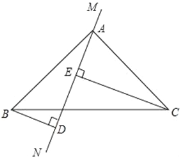
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=AC,直线MN经过点A,过点B作BD⊥MN于D,过C作CE⊥MN于E.
(1)求证:△ABD≌△CAE;
(2)若BD=12cm,DE=20cm,求CE的长度.
相关试题

