搜索
【题目】如图，一段抛物线：y=﹣x（x﹣5）（0≤x≤5），记为C1，它与x轴交于点O，A1；将C1绕点A1旋转180°得C2，交x轴于点A2；将C2绕点A2旋转180°得C3，交x轴于点A3；…如此进行下去，得到一“波浪线”，若点P（2018，m）在此“波浪线”上，则m的值为（ ）
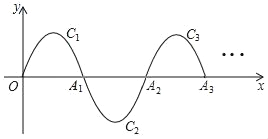
A. 4 B. ﹣4 C. ﹣6 D. 6
参考答案：
【答案】C
【解析】分析：根据图象的旋转变化规律以及二次函数的平移规律得出平移后解析式，进而求出m的值，由2017÷5=403…2，可知点P（2018，m）在此“波浪线”上C404段上，求出C404的解析式，然后把P（2018，m）代入即可．
详解：当y=0时，﹣x（x﹣5）=0，解得x1=0，x2=5，则A1（5，0），
∴OA1=5，
∵将C1绕点A1旋转180°得C2，交x轴于点A2；将C2绕点A2旋转180°得C3，交x轴于点A3；…；如此进行下去，得到一“波浪线”，
∴A1A2=A2A3=…=OA1=5，
∴抛物线C404的解析式为y=（x﹣5×403）（x﹣5×404），即y=（x﹣2015）（x﹣2020），
当x=2018时，y=（2018﹣2015）（2018﹣2020）=﹣6，
即m=﹣6．
故选：C．
-
科目： 来源： 题型：
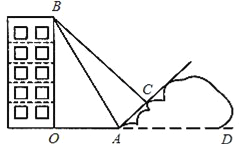
查看答案和解析>>【题目】某校九年级的小红同学，在自己家附近进行测量一座楼房高度的实践活动．如图，她在山坡坡脚A出测得这座楼房的楼顶B点的仰角为60°，沿山坡往上走到C处再测得B点的仰角为45°．已知OA=200m，此山坡的坡比i=
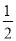，且O、A、D在同一条直线上．求：（1）楼房OB的高度；
（2）小红在山坡上走过的距离AC．（计算过程和结果均不取近似值）
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知y﹣2与x成正比例，当x＝2时，y＝6．
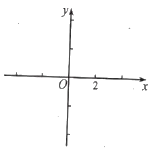
（1）求y与x之间的函数解析式．
（2）在所给直角坐标系中画出函数图象．
（3）由函数图象直接写出当﹣2≤y≤2时，自变量x的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】解方程（组）
（1）2（x﹣1）3+16=0．
（2）
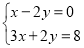；（3）
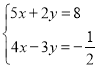． （4）
-
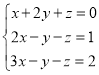
科目： 来源： 题型：
查看答案和解析>>【题目】以下是八（1）班学生身高的统计表和扇形统计图，请回答以下问题.
八（1）班学生身高统计表
组别
身高（单位：米）
人数
第一组
1.85以上
1
第二组
第三组
19
第四组
第五组
1.55以下
8
（1）求出统计表和统计图缺的数据.
（2）八（1）班学生身高这组数据的中位数落在第几组？
（3）如果现在八（1）班学生的平均身高是1.63
，已确定新学期班级转来两名新同学，新同学的身高分别是1.54 和1.77 ，那么这组新数据的中位数落在第几组？ -
科目： 来源： 题型：
查看答案和解析>>【题目】完成下面的证明过程：
如图，AB∥CD，AD∥BC，BE平分∠ABC，DF平分∠ADC．
求证：BE∥DF．
证明：∵AB∥CD，（已知）
∴∠ABC+∠C＝180°．（ ）
又∵AD∥BC，（已知）
∴ +∠C＝180°．（ ）
∴∠ABC＝∠ADC．（ ）
∵BE平分∠ABC，（已知）
∴∠1＝
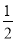∠ABC．（ ）同理，∠2＝
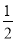∠ADC．∴ ＝∠2．
∵AD∥BC，（已知）
∴∠2＝∠3．（ ）
∴∠1＝∠3，
∴BE∥DF．（ ）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，数轴上的 A 、 B 两点所表示的数分别为 a 、b，a b 0 ，ab 0
（1）原点O 的位置在 ；
A.点 A 的右边 B. 点 B 的左边
C.点 A 与点 B 之间，且靠近点 A D. 点 A 与点 B 之间，且靠近点 B
（2）若 a b 2 ，
①利用数轴比较大小： a 1， b 1 ；（填“>”、“<”或“=”）
②化简：|a-1|+|b+1|.
相关试题
