【题目】完成下面的证明过程:
如图,AB∥CD,AD∥BC,BE平分∠ABC,DF平分∠ADC.
求证:BE∥DF.

证明:∵AB∥CD,(已知)
∴∠ABC+∠C=180°.( )
又∵AD∥BC,(已知)
∴ +∠C=180°.( )
∴∠ABC=∠ADC.( )
∵BE平分∠ABC,(已知)
∴∠1=![]() ∠ABC.( )
∠ABC.( )
同理,∠2=![]() ∠ADC.
∠ADC.
∴ =∠2.
∵AD∥BC,(已知)
∴∠2=∠3.( )
∴∠1=∠3,
∴BE∥DF.( )
参考答案:
【答案】两直线平行,同旁内角互补;∠ADC;两直线平行,同旁内角互补;同角的补角相等;角的平分线的定义;∠1;两直线平行,内错角相等;同位角相等,两直线平行.
【解析】
先由平行线的性质知∠ABC+∠C=∠ADC+∠C=180°知∠ABC=∠ADC,根据角平分线的定义证∠1=∠2,结合AD∥BC得∠2=∠3,根据平行线的性质得∠1=∠3,从而得证.
证明:∵AB∥CD,(已知)
∴∠ABC+∠C=180°.(两直线平行,同旁内角互补)
又∵AD∥BC,(已知)
∴∠ADC+∠C=180°.(两直线平行,同旁内角互补)
∴∠ABC=∠ADC.(同角的补角相等)
∵BE平分∠ABC,(已知)
∴∠1=![]() ∠ABC.(角的平分线的定义)
∠ABC.(角的平分线的定义)
同理,∠2=![]() ∠ADC.
∠ADC.
∴∠1=∠2.
∵AD∥BC,(已知)
∴∠2=∠3.(两直线平行,内错角相等)
∴∠1=∠3,
∴BE∥DF.(同位角相等,两直线平行)
故答案为:两直线平行,同旁内角互补;∠ADC;两直线平行,同旁内角互补;同角的补角相等;角的平分线的定义;∠1;两直线平行,内错角相等;同位角相等,两直线平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程(组)
(1)2(x﹣1)3+16=0.
(2)
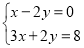 ;
;(3)
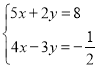 .
. (4)
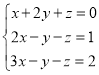
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一段抛物线:y=﹣x(x﹣5)(0≤x≤5),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,得到一“波浪线”,若点P(2018,m)在此“波浪线”上,则m的值为( )
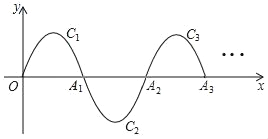
A. 4 B. ﹣4 C. ﹣6 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下是八(1)班学生身高的统计表和扇形统计图,请回答以下问题.
八(1)班学生身高统计表
组别
身高(单位:米)
人数
第一组
1.85以上
1
第二组

第三组

19
第四组

第五组
1.55以下
8

(1)求出统计表和统计图缺的数据.
(2)八(1)班学生身高这组数据的中位数落在第几组?
(3)如果现在八(1)班学生的平均身高是1.63
 ,已确定新学期班级转来两名新同学,新同学的身高分别是1.54
,已确定新学期班级转来两名新同学,新同学的身高分别是1.54  和1.77
和1.77  ,那么这组新数据的中位数落在第几组?
,那么这组新数据的中位数落在第几组? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上的 A 、 B 两点所表示的数分别为 a 、b,a b 0 ,ab 0

(1)原点O 的位置在 ;
A.点 A 的右边 B. 点 B 的左边
C.点 A 与点 B 之间,且靠近点 A D. 点 A 与点 B 之间,且靠近点 B
(2)若 a b 2 ,
①利用数轴比较大小: a 1, b 1 ;(填“>”、“<”或“=”)
②化简:|a-1|+|b+1|.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=4
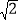 ,则△CEF的周长为_____.
,则△CEF的周长为_____.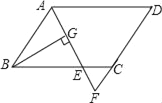
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知 a b , a 与b 两个数在数轴上对应的点分别为点 A 、点 B ,求 A 、 B 两点之间的距离.
(探索)
小明利用绝对值的概念,结合数轴,进行探索:
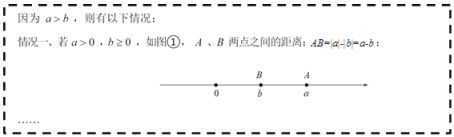
(1)补全小明的探索
(应用)
(2)若点C 对应的数c ,数轴上点C 到A、B 两点的距离相等,求c .(用含a、b 的代数式表示)
(3)若点 D对应的数 d ,数轴上点 D 到 A 的距离是点 D 到 B 的距离的nn 0 倍,请探索 n 的取值范围与点 D 个数的关系,并直接写出a、b 、d、n 的关系.
相关试题

