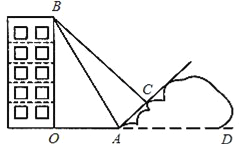
【题目】某校九年级的小红同学,在自己家附近进行测量一座楼房高度的实践活动.如图,她在山坡坡脚A出测得这座楼房的楼顶B点的仰角为60°,沿山坡往上走到C处再测得B点的仰角为45°.已知OA=200m,此山坡的坡比i=![]() ,且O、A、D在同一条直线上.
,且O、A、D在同一条直线上.
求:(1)楼房OB的高度;
(2)小红在山坡上走过的距离AC.(计算过程和结果均不取近似值)
参考答案:
【答案】(1)200![]() m;(2)
m;(2) m.
m.
【解析】试题分析:(1)由在Rt△ABO中,∠BAO=60°,OA=200,则可得tan60°=![]() ,则利用正切函数的知识即可求得答案;
,则利用正切函数的知识即可求得答案;
(2)首先过点C作CE⊥BO于E,CH⊥OD于H,由题意可知i=![]() ,然后设CH=x,AH=2x,在Rt△BEC中,∠BCE=45°,利用直角三角形的性质,即可得方程:200
,然后设CH=x,AH=2x,在Rt△BEC中,∠BCE=45°,利用直角三角形的性质,即可得方程:200![]() ﹣x=200+2x,由在Rt△ACH中,利用勾股定理即可求得答案.
﹣x=200+2x,由在Rt△ACH中,利用勾股定理即可求得答案.
解:(1)在Rt△ABO中,∠BAO=60°,OA=200.
∵tan60°=![]() ,
,
即![]() ,
,
∴OB=![]() OA=200
OA=200![]() (m).
(m).
(2)如图,过点C作CE⊥BO于E,CH⊥OD于H.

则OE=CH,EC=OH.
根据题意,知i=![]() ,
,
可设CH=x,AH=2x. …
在Rt△BEC中,∠BCE=45°,
∴BE=CE,
即OB﹣OE=OA+AH.
∴200![]() ﹣x=200+2x.
﹣x=200+2x.
解得x= . …
. …
在Rt△ACH中,
∵AC2=AH2+CH2,
∴AC2=(2x)2+x2=5x2.
∴AC=![]() x=
x=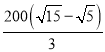 (m).
(m).
答:高楼OB的高度为200![]() m,小玲在山坡上走过的距离AC为
m,小玲在山坡上走过的距离AC为 m.
m.
-
科目: 来源: 题型:
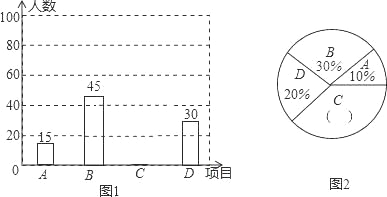
查看答案和解析>>【题目】为进一步推广“阳光体育”大课间活动,某中学对已开设的A实心球,B立定跳远,C跑步,D跳绳四种活动项目的学生喜欢情况进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2的统计图,请结合图中的信息解答下列问题:
(1)请计算本次调查中喜欢“跑步”的学生人数和所占百分比,并将两个统计图补充完整;
(2)随机抽取了5名喜欢“跑步”的学生,其中有3名女生,2名男生,现从这5名学生中任意抽取2名学生,请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若把代数式x2-2x+3化为(x-m)2+k的形式,其中m,k为常数,结果正确的是( )
A. (x+1)2+4 B. (x-1)2+2 C. (x-1)2+4 D. (x+1)2+2
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A. 两条平行线被第三条直线所截,同位角的平分线互相平行
B. 两条平行线被第三条直线所截,同旁内角的平分线互相平行
C. 同一平面内,垂直于同一条直线的两直线平行
D. 同一平面内无公共点的两直线必平行
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列选项,能说明命题“任何偶数都是8的整数倍”是假命题的反例是( )
A. 2k(k为常数) B. 15 C. 24 D. 42
-
科目: 来源: 题型:
查看答案和解析>>【题目】某病毒的直径为0.00000016m,用科学计数法表示为______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对八(2)班的一次考试成绩进行统计,已知75.5~85.5分这一组的频数是9,频率是0.2,那么该班级的人数是 人.
相关试题

