【题目】已知点A(3,4),点B(﹣1,1),在x轴上有两动点E、F,且EF=1,线段EF在x轴上平移,当四边形ABEF的周长取得最小值时,点E的坐标为________.
参考答案:
【答案】(﹣![]() ,0)
,0)
【解析】如图,过点A作x轴的平行线,并且在这条平行线上截取线段AA′,使AA′=1,作点B关于x轴的对称点B′,连接A′B′,交x轴于点E,在x轴上截取线段EF=1,则此时四边形ABEF的周长最小.
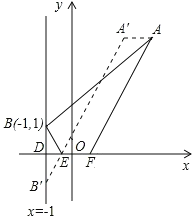
∵A(3,4),∴A′(2,4),
∵B(-1,1),∴B′(-1,-1).
设直线A′B′的解析式为y=kx+b,
则![]() ,
,
解得,k=![]() ,b=
,b=![]() .
.
∴直线A′B′的解析式为y=![]() x+
x+![]() ,
,
当y=0时, ![]() x+
x+![]() =0,解得x=-
=0,解得x=-![]() .
.
故线段EF平移至如图所示位置时,四边形ABEF的周长最小,此时点E的坐标为(-![]() ,0).
,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格中每个小正方形的顶点叫格点,△OAB的顶点的坐标分别为O(0,0)、A(1,3)、B(5,0).
(1)请画出与△OAB关于原点对称的△OCD;(其中A的对称点为C,B的对称点为D)
(2)在(1)的条件下,连接BC、DA,请画出一条直线MN(不与直线AC和坐标轴重合),将四边形ABCD的面积分成相等的两部分,其中M、N分别在AD和BC上,且M、N均为格点,并直接写出直线MN的解析式(写出一个即可).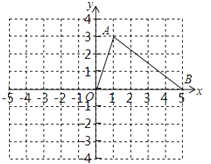
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小平为了测量学校教学楼的高度,她先在A处利用测角仪测得楼顶C的仰角为30°,再向楼的方向直行50米到达B处,又测得楼顶C的仰角为60度.已知测角仪的高度是1.2米,请你帮助小平计算出学校教学楼的高度CO.(
 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知
 ,
,  与
与 互余,
互余,  平分
平分 .
.(1)在图1中,若
 ,则
,则 ______
______ ,
,  ______
______ .
.(2)在图1中,设
 ,
,  ,请探究
,请探究 与
与 之间的数量关系(必须写出推理的主要过程,但每一步后面不必写出理由);
之间的数量关系(必须写出推理的主要过程,但每一步后面不必写出理由);(3)在已知条件不变的前提下,当
 绕着点O顺时针转动到如图2的位置,此时
绕着点O顺时针转动到如图2的位置,此时 与
与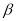 之间的数量关系是否还成立?若成立,请说明理由;若不成立,请直接写出此时
之间的数量关系是否还成立?若成立,请说明理由;若不成立,请直接写出此时 与
与 之间的数量关系.
之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在菱形ABCD中,∠ADC=60°,点H为CD上任意一点(不与C、D重合),过点H作CD的垂线,交BD于点E,连接AE.
(1)如图1,线段EH、CH、AE之间的数量关系是;
(2)如图2,将△DHE绕点D顺时针旋转,当点E、H、C在一条直线上时,求证:AE+EH=CH
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)某种手机卡的市话费上次已按原收费标准降低了m元/分钟,现在再次下调20%,使收费标准为n元/分钟,那么原收费标准为____元/分钟;
(2)买一个篮球需要m元,买一个排球需要n元,则买3个篮球和5个排球共需要____元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小李按市场价格30元/千克收购了一批海鲜1000千克存放在冷库里,据预测,海鲜的市场价格将每天每千克上涨1元.冷冻存放这批海鲜每天需要支出各种费用合计310元,而且这些海鲜在冷库中最多存放160天,同时平均每天有3千克的海鲜变质.
(1)设x天后每千克该海鲜的市场价格为y元,试写出y与x之间的函数关系式;
(2)若存放x天后,将这批海鲜一次性出售.设这批海鲜的销售总额为P元,试写出P与x之间的函数关系式;
(3)小李将这批海鲜存放多少天后出售可获得最大利润,最大利润是多少元?(利润W=销售总额﹣收购成本﹣各种费用)
相关试题

