【题目】如图,在Rt△ABC中,∠ABC=90°,BC=1,AC=![]() .
.
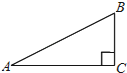
(1)以点B为旋转中心,将△ABC沿逆时针方向旋转90°得到△A′BC′,请画出变换后的图形;
(2)求点A和点A′之间的距离.
参考答案:
【答案】(1)见解析;(2)2![]()
【解析】
试题分析:(1)在BA上截取BC′=BC,延长CB到A′使BA′=BA,然后连结A′C′,则△A′BC′满足条件;
(2)先利用勾股定理计算出AB=2,再利用旋转的性质得BA=BA′,∠ABA′=90°,然后根据等腰直角三角形的性质计算AA′的长即可.
解:(1)如图,△A′BC′为所作;
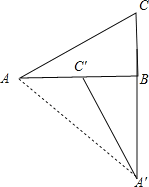
(2)∵∠ABC=90°,BC=1,AC=![]() ,
,
∴AB=![]() =2,
=2,
∵△ABC沿逆时针方向旋转90°得到△A′BC′,
∴BA=BA′,∠ABA′=90°,
∴△ABA′为等腰直角三角形,
∴AA′=![]() AB=2
AB=2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】五名学生投篮球,规定每人投20次,统计他们每人投中的次数,得到五个数据.若这五个数据的中位数是6,唯一众数是7,则他们投中次数的总和可能是( )
A. 20 B. 28 C. 30 D. 31
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市统计部门公布的2016年6~10月份本市居民消费价格指数(CPI)的同比增长分别为2.3%,2.3%,2%,1.6%,1.6%,业内人士评论说:“这五个月的本市居民消费价格指数同比增长率之间相当平稳”,从统计角度看,“增长率之间相当平稳”反映的统计量是( )
A. 方差 B. 平均数 C. 众数 D. 中位数
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=mx2﹣(m+2)x+2(m≠0).
(1)求证:此二次函数的图象与x轴总有交点;
(2)如果此二次函数的图象与x轴两个交点的横坐标都是整数,求正整数m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个正数的两个平方根分别是3a+2和a+14,则这个正数是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:
如果y′=
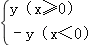 ,那么称点Q为点P的“关联点”.
,那么称点Q为点P的“关联点”.例如:点(5,6)的“关联点”为点(5,6),点(﹣5,6)的“关联点”
为点(﹣5,﹣6).
(1)①点(2,1)的“关联点”为 ;②如果点A(3,﹣1),B(﹣1,3)的“关联点”中有一个在函数
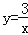 的图象上,那么这个点是 (填“点A”或“点B”).
的图象上,那么这个点是 (填“点A”或“点B”).(2)①如果点M*(﹣1,﹣2)是一次函数y=x+3图象上点M的“关联点”,
那么点M的坐标为 ;②如果点N*(m+1,2)是一次函数y=x+3图象上点N的“关联点”,求点N的坐标.
(3)如果点P在函数y=﹣x2+4(﹣2<x≤a)的图象上,其“关联点”Q的纵坐标
y′的取值范围是﹣4<y′≤4,那么实数a的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】“a的2倍与1的和”用代数式表示是 .
相关试题

