【题目】在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:
如果y′=![]() ,那么称点Q为点P的“关联点”.
,那么称点Q为点P的“关联点”.
例如:点(5,6)的“关联点”为点(5,6),点(﹣5,6)的“关联点”
为点(﹣5,﹣6).
(1)①点(2,1)的“关联点”为 ;②如果点A(3,﹣1),B(﹣1,3)的“关联点”中有一个在函数![]() 的图象上,那么这个点是 (填“点A”或“点B”).
的图象上,那么这个点是 (填“点A”或“点B”).
(2)①如果点M*(﹣1,﹣2)是一次函数y=x+3图象上点M的“关联点”,
那么点M的坐标为 ;②如果点N*(m+1,2)是一次函数y=x+3图象上点N的“关联点”,求点N的坐标.
(3)如果点P在函数y=﹣x2+4(﹣2<x≤a)的图象上,其“关联点”Q的纵坐标
y′的取值范围是﹣4<y′≤4,那么实数a的取值范围是 .
参考答案:
【答案】(1)(2,1),B;(2)(﹣1,2),(﹣1,﹣2);(3)﹣2<a<2.
【解析】
试题分析:(1)根据在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:如果y′=![]() ,那么称点Q为点P的“关联点”,可得答案;
,那么称点Q为点P的“关联点”,可得答案;
(2)在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:如果y′=![]() ,那么称点Q为点P的“关联点”,可得答案;
,那么称点Q为点P的“关联点”,可得答案;
(3)根据在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:如果y′=![]() ,那么称点Q为点P的“关联点”,可得P点自变量的取值范围,可得答案.
,那么称点Q为点P的“关联点”,可得P点自变量的取值范围,可得答案.
解:(1)①点(2,1)的“关联点”为(2,1);
②如果点A(3,﹣1)的关联点为(3,﹣1);
B(﹣1,3)的“关联点”为(﹣1,﹣3),
一个在函数![]() 的图象上,那么这个点是 B;
的图象上,那么这个点是 B;
故答案为:(2,1),B;
(2)①如果点M*(﹣1,﹣2)是一次函数y=x+3图象上点M的“关联点”是(﹣1,2),
那么点M的坐标为(﹣1,2);
②如果点N*(m+1,2)是一次函数y=x+3图象上,
点N*(﹣1,2)的“关联点”(﹣1,﹣2),
点N的坐标是(﹣1,﹣2),
故答案为:(﹣1,2),(﹣1,﹣2);
(3)如果点P在函数y=﹣x2+4(﹣2<x≤a)的图象上,
当﹣2<x≤0时,0<y≤4,即﹣2<a≤0;
当x>0时,y=y′,即﹣4<y≤4,
﹣x2+4>﹣4,解得x<2![]() ,
,
即0<x<2![]() ,
,
综上所述:﹣2<x<2![]() ,
,
﹣2<a<2![]() .
.
“关联点”Q的纵坐标y′的取值范围是﹣4<y′≤4,那么实数a的取值范围是﹣2<a<2![]() ,
,
故答案为:﹣2<a<2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=mx2﹣(m+2)x+2(m≠0).
(1)求证:此二次函数的图象与x轴总有交点;
(2)如果此二次函数的图象与x轴两个交点的横坐标都是整数,求正整数m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,BC=1,AC=
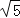 .
.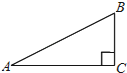
(1)以点B为旋转中心,将△ABC沿逆时针方向旋转90°得到△A′BC′,请画出变换后的图形;
(2)求点A和点A′之间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个正数的两个平方根分别是3a+2和a+14,则这个正数是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“a的2倍与1的和”用代数式表示是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P的坐标为(5,﹣12),则点P到x轴的距离为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2+2x﹣3的图象的顶点坐标 ,对称轴是直线 ,最小值是 .
相关试题

