【题目】在正方形![]() 中,点
中,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,点
,点![]() 为
为![]() 边上一点,连接
边上一点,连接![]() ,作
,作![]() 交直线
交直线![]() 于点
于点![]() .
.
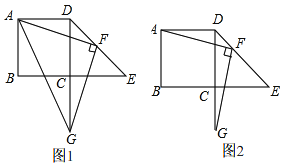
(1)如图1,填空:![]() _____________;
_____________;
(2)如图1,连接![]() ,若
,若![]() ,求
,求![]() 的面积;
的面积;
(3)如图2,若![]() 时,求证:DG=
时,求证:DG=![]() +AD.
+AD.
参考答案:
【答案】(1)135°;(2)20;(3)见解析
【解析】
(1)根据题意得出∠ADC=90°,∠CDE=45°,即可得出结果;
(2)先判断出∠ADF=∠GCF,进而得出△ADF≌△GCF,可得△AFG是等腰直角三角形,过F作FH⊥AD,交AD延长线于H,利用勾股定理和等腰三角形的性质求出AF和FG,即可得到△AFG的面积;
(3)过点F作FM⊥DE,证明△ADF≌△GMF,得出AD=MG,最后用等量代换即可得到结果.
解:(1)∵四边形ABCD为正方形,
∴∠ADC=∠DCB=∠DCE=90°,
∵CE=CD,
∴∠CDE=∠CED=45°,
∴∠ADE=90°+45°=135°;
(2)如图1,连接CF,
在Rt△CDE中,CE=CD,DF=EF,
∴CF=DF=EF,∠ECF=∠CDE=45°,
∴∠FCG=∠GCE+∠ECF=135°,
∴∠ADF=∠GCF=135°,
∵AF⊥FG,CF⊥DE,
∴∠AFG=∠DFC=90°,
∴∠AFD=∠GFC,
在△ADF和△GCF中,
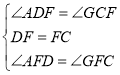 ,
,
∴△ADF≌△GCF(ASA),
∴AF=FG,
∵∠AFG=90°,
∴△AFG是等腰直角三角形,
过F作FH⊥AD,交AD延长线于H,
可知∠FDH=45°,即△FDH为等腰直角三角形,
设HF=DH=x,
∵AD=4=CD,
∴DE=![]() ,
,
∴DF=![]() ,
,
∴![]() ,
,
解得x=2,即DH=HF=2,AH=6,
∴在△AFH中,
AF=![]() =FG,
=FG,
∴S△AFG=![]() =20;
=20;
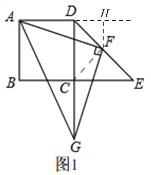
(3)如图2,过点F作FM⊥DE,
由(1)知,∠CDE=45°,
∴△DFM为等腰直角三角形,
∴DM=![]() DF,DF=MF,∠DMF=45°,
DF,DF=MF,∠DMF=45°,
∴∠GMF=135°=∠ADF,
∵MF⊥DE,
∴∠DFM=90°,
又∵∠AFG=90°,
∴∠AFD=∠GFM,
在△ADF和△GMF中,
 ,
,
∴△ADF≌△GMF(ASA),
∴AD=MG,
∴DG=DM+MG=![]() DF+AD.
DF+AD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强学生课外阅读,开阔视野,某校开展了“书香校园,从我做起”的主题活动.学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制出频数分布表和频数分布直方图的一部分如下:
课外阅读时间(单位:小时)
频数(人数)
频率
0﹤t≤2
2
0.04
2﹤t≤4
3
0.06
4﹤t≤6
15
0.30
6﹤t≤8
a
0.50
t﹥8
5
b

请根据图表信息回答下列问题:
(1)频数分布表中的a=b=;
(2)将频数分布直方图补充完整;
(3)学校将每周课外阅读时间在8小时以上的学生评为“阅读之星”,请你估计该校2000名学生中评为“阅读之星”的有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】在横线上完成下面的证明,并在括号内注明理由.
已知:如图,∠ABC+∠BGD=180°,∠1=∠2.
求证:EF∥DB.
证明:∵∠ABC+∠BGD=180°,(已知)
∴ .( )
∴∠1=∠3.( )
又∵∠1=∠2,(已知)
∴ .( )
∴EF∥DB.( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】A,B两地被大山阻隔,若要从A地到B地,只能沿着如图所示的公路先从A地到C地,再由C地到B地.现计划开凿隧道A,B两地直线贯通,经测量得:∠CAB=30°,∠CBA=45°,AC=20km,求隧道开通后与隧道开通前相比,从A地到B地的路程将缩短多少?(结果精确到0.1km,参考数据:
 ≈1.414,
≈1.414,  ≈1.732)
≈1.732)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
 的方程
的方程  有两个实数根
有两个实数根 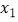 、
、  .
.
(1)求实数k的取值范围;
(2)若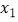 、
、  满足
满足  ,求实数
,求实数 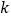 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织了全校1500名学生参加传统文化知识网络竞赛.赛后随机抽取了其中200名学生的成绩作为样本进行整理,并制作了如下不完整的频数分布表和频数分布直方图.
成绩(分)
频数(人)
频率
50≤x<60
10
0.05
60≤x<70
20
n
70≤x<80
m
0.15
80≤x<90
80
0.40
90≤x<100
60
0.30
请根据图表提供的信息,解答下列各题:
(1)表中m= ,n= ,请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段80≤x<90对应扇形的圆心角的度数是 ;
(3)若成绩在80分以上(包括80分)为合格,则参加这次竞赛的1500名学生中成绩合格的大约有多少名?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中
中 ,其中
,其中 ;
;(1)求线段
 的长(用
的长(用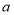 和
和 的代数式表示);
的代数式表示);(2)如图1,若
 ,点
,点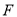 在
在 上,点
上,点 在
在 上,点
上,点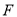 到
到 和BC的距离相等,
和BC的距离相等, ,连接
,连接 ,求
,求 的长;
的长;(3)如图2,若
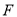 为
为 的中点,
的中点, ,点
,点 分别在线段
分别在线段 上,且
上,且 ,连接
,连接 ,
, 和
和 ,求EF的值;
,求EF的值;
相关试题

