【题目】如图,![]() 中
中![]() ,其中
,其中![]() ;
;
(1)求线段![]() 的长(用
的长(用![]() 和
和![]() 的代数式表示);
的代数式表示);
(2)如图1,若![]() ,点
,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,点
上,点![]() 到
到![]() 和BC的距离相等,
和BC的距离相等,![]() ,连接
,连接![]() ,求
,求![]() 的长;
的长;
(3)如图2,若![]() 为
为![]() 的中点,
的中点,![]() ,点
,点![]() 分别在线段
分别在线段![]() 上,且
上,且![]() ,连接
,连接![]() ,
,![]() 和
和![]() ,求EF的值;
,求EF的值;

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据勾股定理计算即可;
(2)过F作FM⊥AC于M,FN⊥BC于N,证明四边形FNCM为正方形,利用FN∥AC,得到![]() ,解出正方形的边长,运用勾股定理可求出DF的长;
,解出正方形的边长,运用勾股定理可求出DF的长;
(3)过F作FG⊥AC于点G,根据已知条件证明△ECD≌△DGF,得到条件证明△EDF为等腰直角三角形,再根据等腰直角三角形的性质可求得结果.
解:(1)根据勾股定理,∵BC=a,AC=b,∠ACB=90°,
∴AB=![]() ;
;
(2)由题意可得:BC=6,AC=8,
∴AB=![]() ,
,
过F作FM⊥AC于M,FN⊥BC于N,
∵F到AC和BC距离相等,
可得四边形FNCM为正方形,
设CM=CN=FN=FM=x,
∵FN⊥BC,AC⊥BC,
∴FN∥AC,
∴![]() ,即
,即![]() ,
,
解得:x=![]() ,
,
∴AM=8-x=![]() ,
,
∵AF=AD,
∴AF=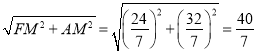 =AD,
=AD,
∴DM=AD-AM=![]() ,
,
∴DF= ;
;

(3)由题意可得:BC=6,AC=8,
∴AB=![]() ,
,
∵F为AB中点,
∴AF=BF=5,
过F作FG⊥AC于点G,
∴FG=![]() BC=3,
BC=3,
∴AG=![]() ,
,
∵BE=BF,AF=AD,
∴BE=5,CE=1,AD=5,CD=3,DG=AD-AG=1,
在△ECD和△DGF中,
 ,
,
∴△ECD≌△DGF(SAS),
∴ED=FD,∠EDC=∠DFG,
∵∠DFG+∠FDG=90°,
∴∠EDC+∠FDG=90°,
∴∠EDF=90°,
∴△EDF为等腰直角三角形,
∵EC=1,CD=3,
∴ED=![]() =FD,
=FD,
∴EF=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形
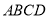 中,点
中,点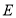 在
在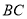 的延长线上,且
的延长线上,且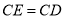 ,点
,点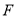 为
为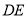 边上一点,连接
边上一点,连接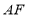 ,作
,作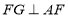 交直线
交直线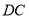 于点
于点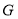 .
.(1)如图1,填空:
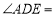 _____________;
_____________;(2)如图1,连接
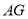 ,若
,若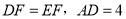 ,求
,求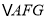 的面积;
的面积;(3)如图2,若
 时,求证:DG=
时,求证:DG=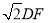 +AD.
+AD.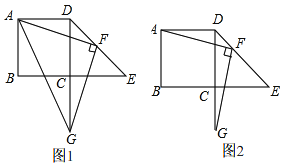
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
 的方程
的方程  有两个实数根
有两个实数根 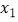 、
、  .
.
(1)求实数k的取值范围;
(2)若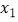 、
、  满足
满足  ,求实数
,求实数 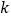 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织了全校1500名学生参加传统文化知识网络竞赛.赛后随机抽取了其中200名学生的成绩作为样本进行整理,并制作了如下不完整的频数分布表和频数分布直方图.
成绩(分)
频数(人)
频率
50≤x<60
10
0.05
60≤x<70
20
n
70≤x<80
m
0.15
80≤x<90
80
0.40
90≤x<100
60
0.30
请根据图表提供的信息,解答下列各题:
(1)表中m= ,n= ,请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段80≤x<90对应扇形的圆心角的度数是 ;
(3)若成绩在80分以上(包括80分)为合格,则参加这次竞赛的1500名学生中成绩合格的大约有多少名?

-
科目: 来源: 题型:
查看答案和解析>>【题目】新园小区计划在一块长为20米,宽12米的矩形场地上修建三条互相垂直的长方形甬路(一条橫向、两条纵向,且横向、纵向的宽度比为3:2),其余部分种花草.若要使种花草的面积达到144米2.则横向的甬路宽为_____米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有大小两种货车,已知1辆大货车与3辆小货车一次可以运货14吨,2辆大货车与5辆小货车一次可以运货25吨.
(1)1辆大货车与1辆小货车一次可以运货各多少吨?
(2)1辆大货车一次费用为300元,1辆小货车一次费用为200元,要求两种货车共用10辆,两次完成80吨的运货任务,且总费用不超过5400元,有哪几种用车方案?请指出费用最低的一种方案,并求出相应的费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b(k≠0)与反比例函数y=
 (m≠0)的图象有公共点A(1,a)、D(﹣2,﹣1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C.
(m≠0)的图象有公共点A(1,a)、D(﹣2,﹣1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C.
(1)求一次函数与反比例函数的解析式;
(2)根据图象回答,x在什么范围内,一次函数的值大于反比例函数的值;
(3)求△ABC的面积.
相关试题

