【题目】(14分)如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连结BE、CE.
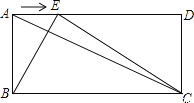
(1)若a=5,AC=13,求b.
(2)若a=5,b=10,当BE⊥AC时,求出此时AE的长.
(3)设AE=x,试探索点E在线段AD上运动过程中,使得△ABE与△BCE相似时,求a、b应满足什么条件,并求出此时x的值.
参考答案:
【答案】(1)b = 12 ;(2)![]() ;(3)
;(3)![]()
【解析】试题分析:(1)在矩形ABCD中,得到∠ABC=90°,利用勾股定理即可计算出结果.
(2)由∵BE⊥AC得到∠2+∠3=90°,由于∠1+∠3=90°,等量代换得到∠1=∠2,推出![]() 得到比例式,即可得到结论;
得到比例式,即可得到结论;
(3)点![]() 在线段
在线段![]() 上的任一点,且不与
上的任一点,且不与![]() 重合,当
重合,当![]() 与
与![]() 相似时,则
相似时,则![]() 当
当![]() (如图2),
(如图2),![]() 又
又![]() 由平行线的性质得到
由平行线的性质得到![]() 推出
推出![]() 得到比例式,进而可得得到一元二次方程
得到比例式,进而可得得到一元二次方程![]() 根据方程根的情况,得到结论.
根据方程根的情况,得到结论.
试题解析:(1)∵四边形ABCD是矩形,
![]()
∵AB=a=5, AC=13,
![]()
∴b=12;
![]() 如图1,∵BE⊥AC
如图1,∵BE⊥AC
![]()
又![]()
∴∠1 = ∠2,

又![]()
∴△AEB ∽△BAC,
∴![]() 即
即![]() ,
,
∴![]() .
.
(3)∵点E在线段AD上的任一点,且不与A、D重合,
∴当△ABE与△BCE相似时,则![]()
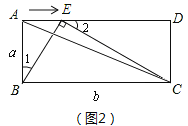
所以当△BAE ∽△CEB(如图2)
则∠1 = ∠BCE,
又BC∥AD,
∴∠2 = ∠BCE,
∴∠1 = ∠2 ,
又![]()
∴△BAE ∽△EDC,
∴![]() 即
即![]() ,
,
∴![]() ,
,
即![]() ,
,
当![]() ,
,
∵a>0,b>0, ∴![]()
即 ![]() 时,
时, ![]() .
.
综上所述:当a、b满足条件b = 2a时△BAE ∽△CEB,此时![]() (或x = a);
(或x = a);
当a、b满足条件b>2a时△BAE ∽△CEB,此时![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为________厘米/秒.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,A(﹣3,﹣2)、B(﹣1,﹣4)
(1)直接写出:S△OAB= ;
(2)延长AB交y轴于P点,求P点坐标;
(3)Q点在y轴上,以A、B、O、Q为顶点的四边形面积为6,求Q点坐标.

-
科目: 来源: 题型:
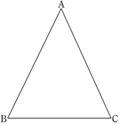
查看答案和解析>>【题目】如图所示,在△ABC中,∠ABC=∠ACB.
(1)尺规作图:过顶点A,作△ABC的角平分线AD;(不写作法,保留作图痕迹)
(2)在AD上任取一点E,连接BE、CE.求证:BE=CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程组:(1)
 ; (2)
; (2)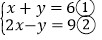 ;
;(3)
 ; (4)
; (4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A.0的平方根是0B.5是25的算术平方根
C.﹣8的立方根是﹣2D.带根号的数都是无理数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3,∠2=∠4.
(1)如图①,求证:DE∥BC;
(2)若将图①改变为图②,其他条件不变,(1)中的结论是否仍成立?请说明理由.
如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3,∠2=∠4.
(1)如图①,求证:DE∥BC;
(2)若将图①改变为图②,其他条件不变,(1)中的结论是否仍成立?请说明理由.


相关试题

