【题目】如图![]() ,以
,以![]() 边
边![]() 和
和![]() 为边作等边
为边作等边![]() 和
和![]() ,连接
,连接![]() ,
,![]() ,
,
![]() 判断
判断![]() 与
与![]() 的数量关系,并求
的数量关系,并求![]() 与
与![]() 的夹角
的夹角![]() 的度数;
的度数;
![]() 继续探索,如图
继续探索,如图![]() ,以
,以![]() 的
的![]() 和
和![]() 为边作正方形
为边作正方形![]() 和
和![]() ,连接
,连接![]() 、
、![]() ,判断
,判断![]() 和
和![]() 的数量关系,并求出此时
的数量关系,并求出此时![]() 与
与![]() 的夹角;
的夹角;
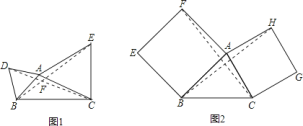
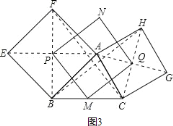
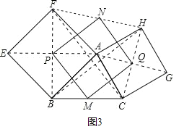
![]() 如图
如图![]() 中
中![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,![]() 、
、![]() 分别是正方形的中心,顺次连接
分别是正方形的中心,顺次连接![]() ,判断四边形
,判断四边形![]() 的形状并证明.
的形状并证明.
参考答案:
【答案】(1)![]() ,
,![]() 的度数为
的度数为![]() ;(2)
;(2)![]() 且
且![]() 与
与![]() 的夹角为
的夹角为![]() ;(3) 四边形
;(3) 四边形![]() 为正方形,理由详见解析.
为正方形,理由详见解析.
【解析】
(1)根据等边三角形的性质可得AB=AD,AE=AC,∠BAD=∠CAE=60°,再求出∠BAE=∠DAC,然后利用“边角边”证明△ABE和△ADC全等,根据全等三角形对应边相等可得BE=DC,全等三角形对应角相等可得∠AEB=∠ACD,然后∠FEC+∠FCE=120°,再根据三角形内角和定理计算即可得解;(2)根据正方形的性质可得AB=AF,AC=AH,∠BAF=∠CAH=90°,再求出∠BAH=∠CAF,然后利用“边角边”证明△ABH和△AFC全等,根据全等三角形对应边相等可得BH=FC,全等三角形对应角相等可得∠AFC=∠ABH,然后∠EFC+∠EBH=180°,设BH、CF相交于点G,再根据四边形的内角和定理计算即可求出∠BGF=90°,根据垂线的定义即可得证;根据正方形的对角线互相平分可得点P、Q分别是BF、CH的中点,再根据三角形的中位线平行于第三边并且等于第三边的一半可得PN∥BH,PN=![]() BH,MQ∥BH,MQ=
BH,MQ∥BH,MQ=![]() BH,NQ∥CF,NQ=
BH,NQ∥CF,NQ=![]() CF,PM∥CF,PM=
CF,PM∥CF,PM=![]() CF,再根据(2)的结论可得BH=CF,BH⊥CF,然后求出MP=PN=NQ=MQ,从而判定四边形MPNQ是菱形,再根据BH⊥CF求出PN⊥NQ,根据有一个角是直角的菱形是正方形证明.
CF,再根据(2)的结论可得BH=CF,BH⊥CF,然后求出MP=PN=NQ=MQ,从而判定四边形MPNQ是菱形,再根据BH⊥CF求出PN⊥NQ,根据有一个角是直角的菱形是正方形证明.
![]() ∵
∵![]() 和
和![]() 都是等边三角形,
都是等边三角形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,
,
在![]() 和
和![]() 中,
中,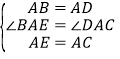 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;

故![]() ,
,![]() 的度数为
的度数为![]() ;
;
![]() 在正方形
在正方形![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,
,
在![]() 和
和![]() 中,
中,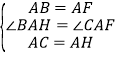 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
设![]() 、
、![]() 相交于点
相交于点![]() ,
,
则![]() ,
,
∴![]() ,
,
故![]() 且
且![]() 与
与![]() 的夹角为
的夹角为![]() ;
;
![]() 四边形
四边形![]() 为正方形.理由如下:
为正方形.理由如下:
∵![]() 、
、![]() 分别是正方形的中心,
分别是正方形的中心,
∴![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,
∵![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
根据![]() 的结论,
的结论,![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形![]() 是菱形,
是菱形,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴菱形![]() 是正方形,
是正方形,
故四边形![]() 为正方形.
为正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线 l 经过点A(2,﹣3),与 x 轴交于点 B,且与直线y=3x-
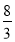 平行.
平行.(1)求直线l的函数解析式及点B的坐标;
(2)如直线l上有一点 M(a,﹣6),过点 M 作 x 轴的垂线,交直线 y=3x-
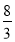 于点N,在线段MN上求一点P,使△PAB是直角三角形,请求出点P的坐标.
于点N,在线段MN上求一点P,使△PAB是直角三角形,请求出点P的坐标.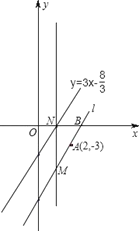
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰 Rt△ABC 中,∠ACB=90°,P 是射线CB上一点(在B点右侧),连接AP,延长PC至点Q,使得 CQ=CP,过点Q作QH⊥AP交PA延长线于点H,交BA延长线于点M,用等式表示线段MB与PQ之间的数量关系,并证明.

-
科目: 来源: 题型:
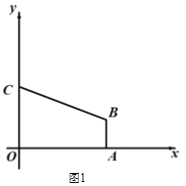
查看答案和解析>>【题目】如图1,在平面直角坐标系中,直角梯形OABC的顶点A的坐标为(4,0),直线y = -
 x + 3经过顶点 B,与y轴交于顶点C,AB // OC.
x + 3经过顶点 B,与y轴交于顶点C,AB // OC.(1)求顶点B的坐标.
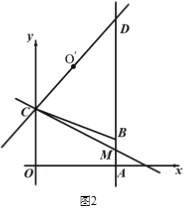
(2)如 图2,直线 L 经过点 C,与直线 AB 交于点 M,点 O′为点 O 关于直线L的对称点,联 结 CO′,并延长交直线AB于第一象限的点 D,当CD=5 时,求直线 L的解析式;
(3)在(2)条件下,点P在直线 L上运动,点Q在直线OD上运动,以 P、Q、B、C 为顶点的四边形能否成为平行四边形?若能,请直接写出点P坐标;若不能,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
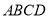 中,
中,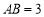 ,
,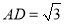 ,点
,点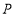 为对角线
为对角线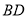 上异于点
上异于点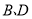 的一个动点,联结
的一个动点,联结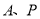 ,将
,将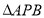 沿
沿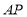 所在的直线翻折,使得点
所在的直线翻折,使得点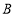 落在点
落在点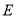 的位置
的位置(1)当
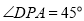 时,求点
时,求点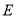 到直线
到直线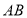 的距离。
的距离。(2)联结
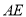 交
交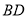 于
于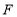 ,求当
,求当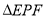 和
和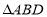 相似时,线段
相似时,线段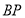 的长。
的长。(3)当
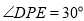 时,请直接写出此时
时,请直接写出此时 的面积。
的面积。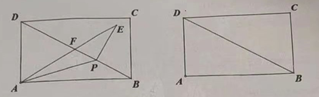
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的顶点O与平面直角坐标系的原点重合,点A,C分别在x轴,y轴上,点B的坐标为(-5,4),点D为边BC上一点,连接OD,若线段OD绕点D顺时针旋转90°后,点O恰好落在AB边上的点E处,则点E的坐标为( )

A. (-5,3) B. (-5,4) C. (-5,
 ) D. (-5,2)
) D. (-5,2) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数
 ,下列说法错误的是( )
,下列说法错误的是( )A. 当x<1时,y随x的增大而减小
B. 若图象与x轴有交点,则

C. 当 a=3时,不等式
 的解集是
的解集是 
D. 若将图象向上平移1个单位,再向左平移3个单位后过点
 ,则 a=3
,则 a=3
相关试题

