【题目】如图,矩形OABC的顶点O与平面直角坐标系的原点重合,点A,C分别在x轴,y轴上,点B的坐标为(-5,4),点D为边BC上一点,连接OD,若线段OD绕点D顺时针旋转90°后,点O恰好落在AB边上的点E处,则点E的坐标为( )

A. (-5,3) B. (-5,4) C. (-5,![]() ) D. (-5,2)
) D. (-5,2)
参考答案:
【答案】A
【解析】
先判定△DBE≌△OCD,可得BD=OC=4,设AE=x,则BE=4﹣x=CD,依据BD+CD=5,可得4+4﹣x=5,进而得到AE=3,据此可得E(﹣5,3).
由题可得:AO=BC=5,AB=CO=4,由旋转可得:DE=OD,∠EDO=90°.
又∵∠B=∠OCD=90°,∴∠EDB+∠CDO=90°=∠COD+∠CDO,∴∠EDB=∠DOC,∴△DBE≌△OCD,∴BD=OC=4,设AE=x,则BE=4﹣x=CD.
∵BD+CD=5,∴4+4﹣x=5,解得:x=3,∴AE=3,∴E(﹣5,3).
故选A.
-
科目: 来源: 题型:
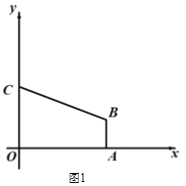
查看答案和解析>>【题目】如图1,在平面直角坐标系中,直角梯形OABC的顶点A的坐标为(4,0),直线y = -
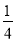 x + 3经过顶点 B,与y轴交于顶点C,AB // OC.
x + 3经过顶点 B,与y轴交于顶点C,AB // OC.(1)求顶点B的坐标.
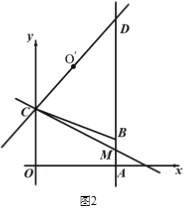
(2)如 图2,直线 L 经过点 C,与直线 AB 交于点 M,点 O′为点 O 关于直线L的对称点,联 结 CO′,并延长交直线AB于第一象限的点 D,当CD=5 时,求直线 L的解析式;
(3)在(2)条件下,点P在直线 L上运动,点Q在直线OD上运动,以 P、Q、B、C 为顶点的四边形能否成为平行四边形?若能,请直接写出点P坐标;若不能,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,以
,以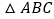 边
边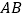 和
和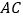 为边作等边
为边作等边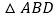 和
和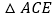 ,连接
,连接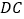 ,
,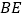 ,
,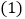 判断
判断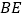 与
与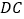 的数量关系,并求
的数量关系,并求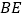 与
与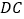 的夹角
的夹角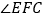 的度数;
的度数;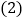 继续探索,如图
继续探索,如图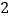 ,以
,以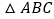 的
的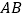 和
和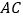 为边作正方形
为边作正方形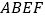 和
和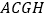 ,连接
,连接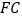 、
、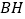 ,判断
,判断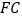 和
和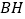 的数量关系,并求出此时
的数量关系,并求出此时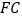 与
与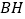 的夹角;
的夹角;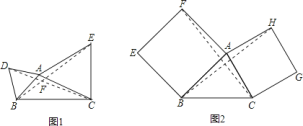
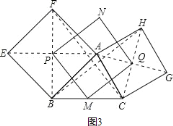
 如图
如图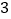 中
中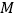 、
、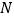 分别是
分别是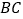 、
、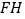 的中点,
的中点,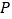 、
、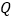 分别是正方形的中心,顺次连接
分别是正方形的中心,顺次连接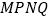 ,判断四边形
,判断四边形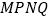 的形状并证明.
的形状并证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
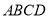 中,
中,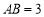 ,
,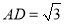 ,点
,点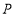 为对角线
为对角线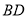 上异于点
上异于点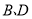 的一个动点,联结
的一个动点,联结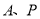 ,将
,将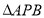 沿
沿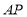 所在的直线翻折,使得点
所在的直线翻折,使得点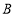 落在点
落在点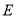 的位置
的位置(1)当
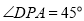 时,求点
时,求点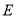 到直线
到直线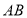 的距离。
的距离。(2)联结
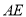 交
交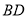 于
于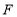 ,求当
,求当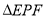 和
和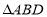 相似时,线段
相似时,线段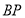 的长。
的长。(3)当
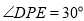 时,请直接写出此时
时,请直接写出此时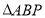 的面积。
的面积。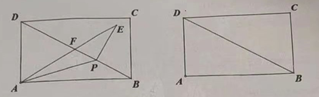
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数
 ,下列说法错误的是( )
,下列说法错误的是( )A. 当x<1时,y随x的增大而减小
B. 若图象与x轴有交点,则

C. 当 a=3时,不等式
 的解集是
的解集是 
D. 若将图象向上平移1个单位,再向左平移3个单位后过点
 ,则 a=3
,则 a=3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形的顶点A(1,1)、B(3,1),规定把等边△ABC“先沿x轴翻折,再向左平移1个单位”为一次变换,如果这样连续经过2018次变换后,等边△ABC的顶点C的坐标为_____.
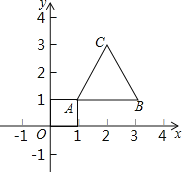
-
科目: 来源: 题型:
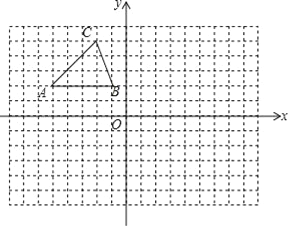
查看答案和解析>>【题目】在如图的方格中,每个小正方形的边长都为1,△ABC的顶点均在格点上.在建立平面直角坐标系后,点B的坐标为(﹣1,2).
(1)把△ABC向下平移8个单位后得到对应的△A1B1C1,画出△A1B1C1;
(2)画出与△A1B1C1关于y轴对称的△A2B2C2;
(3)若点P(a,b)是△ABC边上任意一点,P2是△A2B2C2边上与P对应的点,写出P2的坐标为 ;
(4)试在y轴上找一点Q(在图中标出来),使得点Q到B2、C2两点的距离之和最小,并求出QB2+QC2的最小值.
相关试题

