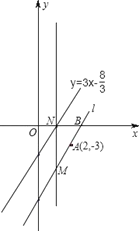
【题目】如图,在平面直角坐标系中,直线 l 经过点A(2,﹣3),与 x 轴交于点 B,且与直线y=3x-![]() 平行.
平行.
(1)求直线l的函数解析式及点B的坐标;
(2)如直线l上有一点 M(a,﹣6),过点 M 作 x 轴的垂线,交直线 y=3x-![]() 于点N,在线段MN上求一点P,使△PAB是直角三角形,请求出点P的坐标.
于点N,在线段MN上求一点P,使△PAB是直角三角形,请求出点P的坐标.
参考答案:
【答案】(1)直线l的解析式为y=3x9,B点坐标为(3,0);(2)P1(1,1),P2(1,2),P3(1, ![]() ).
).
【解析】
(1)设直线l的解析式为:y=kx+b,因为直线l与直线y=3x-![]() 平行,所以k=3,又直线l经过点A(2,-3),从而求出b的值,即可求出直线l的函数解析式及点B的坐标;
平行,所以k=3,又直线l经过点A(2,-3),从而求出b的值,即可求出直线l的函数解析式及点B的坐标;
(2)点M(a,-6)在直线l上,所以可先求出a的值,设点P(1,y),求出y的取值范围,再分情况讨论:当AB为斜边时,当PB为斜边时,当PA为斜边时,利用勾股定理建立方程求解即可.
解:(1)设直线l的解析式为y=kx+b(k≠0),
∵直线l平行于y=3x-![]() ,
,
∴k=3,
∵直线l经过点A(2,3),
∴3=3×2+b,b=9,
∴直线l的解析式为y=3x9,
当y=0时,x=3,
∴点B坐标为(3,0);
(2)∵点M(a,6)在直线l上,
∴3a-9=-6
∴a=1,则可设点P(1,y),
当x=1时,![]() =
=![]()
∴N(1,![]() ),
),
∴y的取值范围是6≤y≤![]() ,
,
∵P(1,y),A(2,-3),B (3,0)
∴![]() ,
,
![]()
![]()
当AB为斜边时,PA2+PB2=AB2,即![]() ,
,
整理得![]() ,解得y1=1,y2=2,
,解得y1=1,y2=2,
∴P1(1,1),P2(1,2),
当PB为斜边时,PA2+AB2=PB2,![]() ,
,
解得![]() ,
,
∴P3(1, ![]() ),
),
当PA为斜边时,PB2+AB2=PA2,即![]() ,
,
解得y=![]() ,
,
∵6≤y≤![]() ,故y=
,故y=![]() 不符合题意,舍去.
不符合题意,舍去.
∴综上所述,点P的坐标为P1(1,1),P2(1,2),P3(1, ![]() ).
).
-
科目: 来源: 题型:
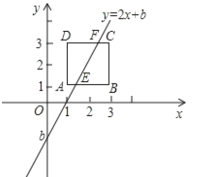
查看答案和解析>>【题目】如图,已知正方形ABCD的顶点A(1,1),B(3,1),直线y=2x+b交边AB于点E,交边CD于点F,则直线y=2x+b 在y 轴上的截距b的变化范围是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,O为原点,点A、C 的坐标分别为(2,0)、(1,3
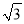 ),将△AOC绕AC的中点旋转180°,点O落到点B的位置,D的坐标为(1,-
),将△AOC绕AC的中点旋转180°,点O落到点B的位置,D的坐标为(1,-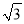 ).若点P是x轴上一点,以P、A、D为顶点作平行四边形,该平行四边形的另一顶点在y轴上,则点P的坐标为_________.
).若点P是x轴上一点,以P、A、D为顶点作平行四边形,该平行四边形的另一顶点在y轴上,则点P的坐标为_________.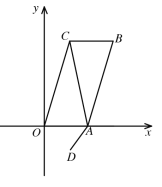
-
科目: 来源: 题型:
查看答案和解析>>【题目】某位篮球运动员在同样的条件下进行投篮练习,结果如下表:
投篮次数




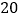



进球次数








进球频率

________
________
________
________
________
________
________
 将上表补充完整;
将上表补充完整; 这位运动员投篮一次,进球的概率约是多少?
这位运动员投篮一次,进球的概率约是多少? 若这位运动员投篮
若这位运动员投篮 次,必定会投进
次,必定会投进 次吗?为什么?
次吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰 Rt△ABC 中,∠ACB=90°,P 是射线CB上一点(在B点右侧),连接AP,延长PC至点Q,使得 CQ=CP,过点Q作QH⊥AP交PA延长线于点H,交BA延长线于点M,用等式表示线段MB与PQ之间的数量关系,并证明.

-
科目: 来源: 题型:
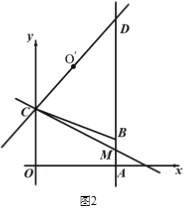
查看答案和解析>>【题目】如图1,在平面直角坐标系中,直角梯形OABC的顶点A的坐标为(4,0),直线y = -
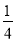 x + 3经过顶点 B,与y轴交于顶点C,AB // OC.
x + 3经过顶点 B,与y轴交于顶点C,AB // OC.(1)求顶点B的坐标.
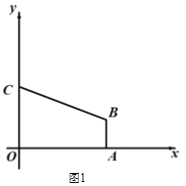
(2)如 图2,直线 L 经过点 C,与直线 AB 交于点 M,点 O′为点 O 关于直线L的对称点,联 结 CO′,并延长交直线AB于第一象限的点 D,当CD=5 时,求直线 L的解析式;
(3)在(2)条件下,点P在直线 L上运动,点Q在直线OD上运动,以 P、Q、B、C 为顶点的四边形能否成为平行四边形?若能,请直接写出点P坐标;若不能,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,以
,以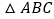 边
边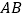 和
和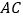 为边作等边
为边作等边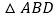 和
和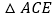 ,连接
,连接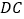 ,
,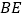 ,
,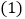 判断
判断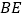 与
与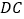 的数量关系,并求
的数量关系,并求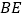 与
与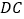 的夹角
的夹角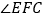 的度数;
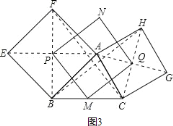
的度数;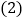 继续探索,如图
继续探索,如图 ,以
,以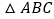 的
的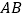 和
和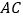 为边作正方形
为边作正方形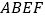 和
和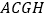 ,连接
,连接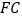 、
、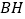 ,判断
,判断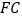 和
和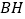 的数量关系,并求出此时
的数量关系,并求出此时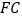 与
与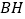 的夹角;
的夹角;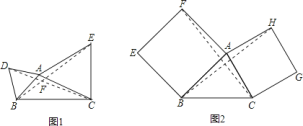
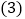 如图
如图 中
中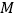 、
、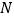 分别是
分别是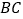 、
、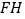 的中点,
的中点,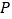 、
、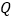 分别是正方形的中心,顺次连接
分别是正方形的中心,顺次连接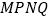 ,判断四边形
,判断四边形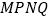 的形状并证明.
的形状并证明.
相关试题

