【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为对角线
为对角线![]() 上异于点
上异于点![]() 的一个动点,联结
的一个动点,联结![]() ,将
,将![]() 沿
沿![]() 所在的直线翻折,使得点
所在的直线翻折,使得点![]() 落在点
落在点![]() 的位置
的位置
(1)当![]() 时,求点
时,求点![]() 到直线
到直线![]() 的距离。
的距离。
(2)联结![]() 交
交![]() 于
于![]() ,求当
,求当![]() 和
和![]() 相似时,线段
相似时,线段![]() 的长。
的长。
(3)当![]() 时,请直接写出此时
时,请直接写出此时![]() 的面积。
的面积。
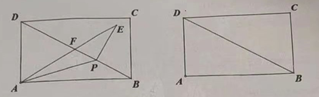
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根据直角三角形性质求解即可
(2)根据题意,相似分为两种情况 ,一是△EPF∽△BAD,二是△EFP∽△BAD,在两种情况下分类讨论,分别求出不同情况下的值
(3)如图一、图二,首先弄清楚题目所存在的情况可能性,之后按照特殊的四边形性质以及三角形相关性质求解即可
解 (1)过E作EG⊥AB于点G,
在Rt△ABD中,AD=![]() , AB=3,
, AB=3,
∴∠ABD =30°,
∵∠APD=45°,
∴∠BAP=15°,
∴∠BAE = 30°
在Rt△EAG中,EA= EB=3
∴EG=![]()
(2)①△EPF∽△BAD,
∴∠EPF = 90° ,
∵∠APB=∠APE,
∴180°-∠APD=90 °+∠APD,
∴∠APD=45°,在△APD中,∠ADP=60°,∠APD=45°,AD=![]() ,DP=
,DP=![]()
∵ BD=![]()
∴BP=![]()
②△EFP∽△BAD,
∴AE⊥BD,
∴∠BAF=60°,
∴∠PAD=30°,
∴AP= BP
在等腰△APB中,AB=3, ∠APB=30°,
∴BP=![]()
综上所述:当△EPF和△ABD相似时,BP=![]() 或
或![]()
(3)

如图一:∠DPE=30°,
∵∠APB=∠APE,
∴180°-∠APD=30°+∠APD,
∴∠APD=75°
∴∠PAB=45°
在△APB中,过P做PI⊥AB
AB=3,∠PAB=45°,∠PBA=30°
∴PI=![]()
∴△APB面积=![]()
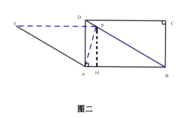
如图二:过P做PH⊥AB于H,易得四边形PEAB为菱形
∴△APB面积=![]()
综上所述,△APB面积为![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰 Rt△ABC 中,∠ACB=90°,P 是射线CB上一点(在B点右侧),连接AP,延长PC至点Q,使得 CQ=CP,过点Q作QH⊥AP交PA延长线于点H,交BA延长线于点M,用等式表示线段MB与PQ之间的数量关系,并证明.

-
科目: 来源: 题型:
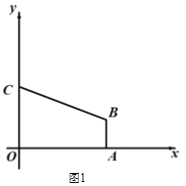
查看答案和解析>>【题目】如图1,在平面直角坐标系中,直角梯形OABC的顶点A的坐标为(4,0),直线y = -
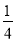 x + 3经过顶点 B,与y轴交于顶点C,AB // OC.
x + 3经过顶点 B,与y轴交于顶点C,AB // OC.(1)求顶点B的坐标.
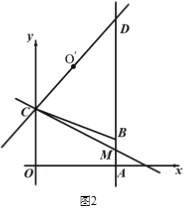
(2)如 图2,直线 L 经过点 C,与直线 AB 交于点 M,点 O′为点 O 关于直线L的对称点,联 结 CO′,并延长交直线AB于第一象限的点 D,当CD=5 时,求直线 L的解析式;
(3)在(2)条件下,点P在直线 L上运动,点Q在直线OD上运动,以 P、Q、B、C 为顶点的四边形能否成为平行四边形?若能,请直接写出点P坐标;若不能,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,以
,以 边
边 和
和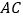 为边作等边
为边作等边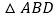 和
和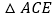 ,连接
,连接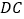 ,
,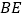 ,
,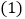 判断
判断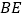 与
与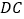 的数量关系,并求
的数量关系,并求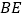 与
与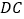 的夹角
的夹角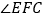 的度数;
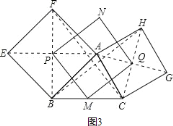
的度数;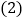 继续探索,如图
继续探索,如图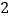 ,以
,以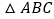 的
的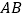 和
和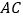 为边作正方形
为边作正方形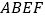 和
和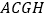 ,连接
,连接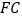 、
、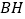 ,判断
,判断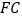 和
和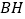 的数量关系,并求出此时
的数量关系,并求出此时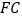 与
与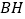 的夹角;
的夹角;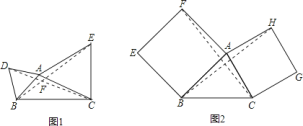
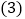 如图
如图 中
中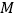 、
、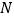 分别是
分别是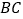 、
、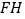 的中点,
的中点,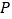 、
、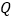 分别是正方形的中心,顺次连接
分别是正方形的中心,顺次连接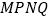 ,判断四边形
,判断四边形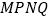 的形状并证明.
的形状并证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的顶点O与平面直角坐标系的原点重合,点A,C分别在x轴,y轴上,点B的坐标为(-5,4),点D为边BC上一点,连接OD,若线段OD绕点D顺时针旋转90°后,点O恰好落在AB边上的点E处,则点E的坐标为( )

A. (-5,3) B. (-5,4) C. (-5,
 ) D. (-5,2)
) D. (-5,2) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数
 ,下列说法错误的是( )
,下列说法错误的是( )A. 当x<1时,y随x的增大而减小
B. 若图象与x轴有交点,则

C. 当 a=3时,不等式
 的解集是
的解集是 
D. 若将图象向上平移1个单位,再向左平移3个单位后过点
 ,则 a=3
,则 a=3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形的顶点A(1,1)、B(3,1),规定把等边△ABC“先沿x轴翻折,再向左平移1个单位”为一次变换,如果这样连续经过2018次变换后,等边△ABC的顶点C的坐标为_____.
相关试题

