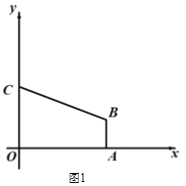
【题目】如图1,在平面直角坐标系中,直角梯形OABC的顶点A的坐标为(4,0),直线y = -![]() x + 3经过顶点 B,与y轴交于顶点C,AB // OC.
x + 3经过顶点 B,与y轴交于顶点C,AB // OC.
(1)求顶点B的坐标.
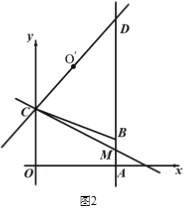
(2)如 图2,直线 L 经过点 C,与直线 AB 交于点 M,点 O′为点 O 关于直线L的对称点,联 结 CO′,并延长交直线AB于第一象限的点 D,当CD=5 时,求直线 L的解析式;
(3)在(2)条件下,点P在直线 L上运动,点Q在直线OD上运动,以 P、Q、B、C 为顶点的四边形能否成为平行四边形?若能,请直接写出点P坐标;若不能,说明理由.
参考答案:
【答案】(1)B(4,2);(2)![]() ;(3)P点坐标为(2,2)或(5,
;(3)P点坐标为(2,2)或(5,![]() )或(-2,4).
)或(-2,4).
【解析】
(1)根据题意设点B的坐标为(4,y),将x=4代入直线解析式即可求出B点纵坐标,从而得到B点坐标;
(2)过C点作CN⊥AB于N,由平行线和对称的性质可推出∠DCM=∠DMC,进而得到CD=MD=5,利用勾股定理求出DN,得到NM=2,易得AM=1,从而得到M点坐标,利用待定系数法即可求出直线L的解析式;
(3)连接OD,先求出OD直线解析式,根据点P在直线 L上运动,点Q在直线OD上运动,可设P点坐标为(![]() ),Q点坐标为(
),Q点坐标为(![]() ),在分类讨论,利用平行四边形对角线互相平分的性质和中点坐标公式可建立方程求解.
),在分类讨论,利用平行四边形对角线互相平分的性质和中点坐标公式可建立方程求解.
解:(1)∵A(4,0),AB∥OC,
∴设点B的坐标为(4,y)
把x=4代入![]() 中,得y=2,
中,得y=2,
∴B(4,2);
(2)如图,过C点作CN⊥AB于N,
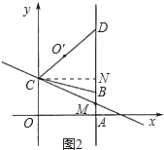
∵AB∥OC,
∴∠OCM=∠DMC,
∵点 O′为点 O 关于直线L的对称点
∴∠DCM=∠OCM,
∴∠DCM=∠DMC
∴CD=MD=5,
∵![]() ,当x=0时y=3,
,当x=0时y=3,
∴OC=3,
∵CN=OA=4,
∴DN=![]() ,
,
∴NM=53=2,
∴AM=AN-NM=3-2=1
∴M(4,1),
设直线L解析式y=kx+b把C(0,3),M(4,1)代入得:
![]() ,解得
,解得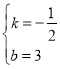 ,
,
∴直线L的解析式为:![]() .
.
(3)如图,连接OD,
∵AD=AM+MD=1+5=6,AD∥OC,A点坐标为(4,0)
∴D点坐标为(4,6)
设OD直线解析式为![]() ,将(4,6)代入可得
,将(4,6)代入可得![]() ,解得
,解得![]()
∴直线OD解析式为![]() ,
,
∵点P在直线 L上运动,点Q在直线OD上运动
∴设P点坐标为(![]() ),Q点坐标为(
),Q点坐标为(![]() ),
),
分情况讨论:
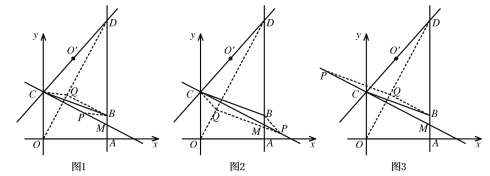
如图1所示,当BC、PQ为对角线时,由平行四边形对角线互相平分的性质和中点坐标公式可得:
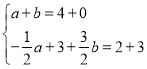 ,解得
,解得![]() ,
,
当![]() 时,
时,![]()
∴P点坐标为(2,2);
如图2所示,当BQ、PC为对角线时,同理可得:
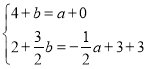 ,解得
,解得![]() ,
,
当![]() 时,
时,![]()
∴P点坐标为(5,![]() );
);
如图3所示,当BP、CQ为对角线时,同理可得:
 ,解得
,解得![]() ,
,
当![]() 时,
时,![]()
∴P点坐标为(-2,4);
综上所述,P点坐标为:(2,2)或(5,![]() )或(-2,4).
)或(-2,4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某位篮球运动员在同样的条件下进行投篮练习,结果如下表:
投篮次数




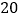



进球次数








进球频率

________
________
________
________
________
________
________
 将上表补充完整;
将上表补充完整; 这位运动员投篮一次,进球的概率约是多少?
这位运动员投篮一次,进球的概率约是多少? 若这位运动员投篮
若这位运动员投篮 次,必定会投进
次,必定会投进 次吗?为什么?
次吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线 l 经过点A(2,﹣3),与 x 轴交于点 B,且与直线y=3x-
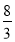 平行.
平行.(1)求直线l的函数解析式及点B的坐标;
(2)如直线l上有一点 M(a,﹣6),过点 M 作 x 轴的垂线,交直线 y=3x-
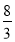 于点N,在线段MN上求一点P,使△PAB是直角三角形,请求出点P的坐标.
于点N,在线段MN上求一点P,使△PAB是直角三角形,请求出点P的坐标.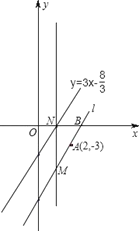
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰 Rt△ABC 中,∠ACB=90°,P 是射线CB上一点(在B点右侧),连接AP,延长PC至点Q,使得 CQ=CP,过点Q作QH⊥AP交PA延长线于点H,交BA延长线于点M,用等式表示线段MB与PQ之间的数量关系,并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
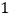 ,以
,以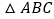 边
边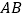 和
和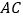 为边作等边
为边作等边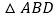 和
和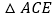 ,连接
,连接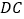 ,
,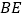 ,
,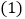 判断
判断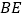 与
与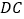 的数量关系,并求
的数量关系,并求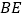 与
与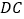 的夹角
的夹角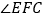 的度数;
的度数; 继续探索,如图
继续探索,如图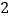 ,以
,以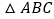 的
的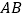 和
和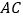 为边作正方形
为边作正方形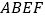 和
和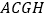 ,连接
,连接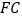 、
、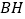 ,判断
,判断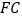 和
和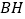 的数量关系,并求出此时
的数量关系,并求出此时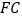 与
与 的夹角;
的夹角;
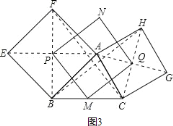
 如图
如图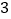 中
中 、
、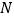 分别是
分别是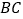 、
、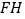 的中点,
的中点,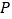 、
、 分别是正方形的中心,顺次连接
分别是正方形的中心,顺次连接 ,判断四边形
,判断四边形 的形状并证明.
的形状并证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 中,
中,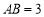 ,
,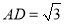 ,点
,点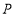 为对角线
为对角线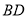 上异于点
上异于点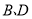 的一个动点,联结
的一个动点,联结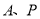 ,将
,将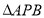 沿
沿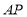 所在的直线翻折,使得点
所在的直线翻折,使得点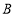 落在点
落在点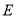 的位置
的位置(1)当
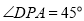 时,求点
时,求点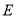 到直线
到直线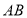 的距离。
的距离。(2)联结
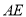 交
交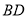 于
于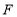 ,求当
,求当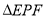 和
和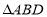 相似时,线段
相似时,线段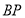 的长。
的长。(3)当
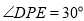 时,请直接写出此时
时,请直接写出此时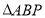 的面积。
的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的顶点O与平面直角坐标系的原点重合,点A,C分别在x轴,y轴上,点B的坐标为(-5,4),点D为边BC上一点,连接OD,若线段OD绕点D顺时针旋转90°后,点O恰好落在AB边上的点E处,则点E的坐标为( )

A. (-5,3) B. (-5,4) C. (-5,
 ) D. (-5,2)
) D. (-5,2)
相关试题

