【题目】已知,一个点从数轴上的原点开始.先向左移动6cm到达A点,再从A点向右移动10cm到达B点,点C是线段AB的中点.
(1)点C表示的数是 ;
(2)若点A以每秒2cm的速度向左移动,同时C、B两点分别以每秒1cm、4cm的速度向右移动,设移动时间为t秒,
①运动t秒时,点C表示的数是 (用含有t的代数式表示);
②当t=2秒时,CBAC的值为 .
③试探索:点A、B、C在运动的过程中,线段CB与AC总有怎样的数量关系?并说明理由.

参考答案:
【答案】(1)-1;(2)①﹣1+t;②121;③线段CB与AC相等,理由详见解析.
【解析】
(1)依据条件即可得到点A表示﹣6,点B表示﹣6+10=4,再根据点C是线段AB的中点,即可得出点C表示的数;
(2)依据点C表示的数为﹣1,点以每秒1cm的速度向右移动,即可得到运动t秒时,点C表示的数是﹣1+t;
②依据点A表示的数为﹣6﹣2×2=﹣10,点B表示的数为4+4×2=12,点C表示的数是﹣1+2=1,即可得到CBAC的值;
③依据点A表示的数为﹣6﹣2t,点B表示的数为4+4t,点C表示的数是﹣1+t,即可得到点A、B、C在运动的过程中,线段CB与AC相等.
解:(1)∵一个点从数轴上的原点开始,先向左移动6cm到达A点,再从A点向右移动10cm到达B点,
∴点A表示﹣6,点B表示﹣6+10=4,
又∵点C是线段AB的中点,
∴点C表示的数为![]() =﹣1,
=﹣1,
故答案为:﹣1.
(2)①∵点C表示的数为﹣1,点以每秒1cm的速度向右移动,
∴运动t秒时,点C表示的数是﹣1+t,
故答案为:﹣1+t;
②由题可得,当t=2秒时,点A表示的数为﹣6﹣2×2=﹣10,点B表示的数为4+4×2=12,点C表示的数是﹣1+2=1,
∴当t=2秒时,AC=11,BC=11,
∴CBAC=121,
故答案为:121;
③点A、B、C在运动的过程中,线段CB与AC相等.理由:
由题可得,点A表示的数为﹣6﹣2t,点B表示的数为4+4t,点C表示的数是﹣1+t,
∴BC=(4+4t)﹣(﹣1+t)=5+3t,AC=(﹣1+t)﹣(﹣6﹣2t)=5+3t,
∴点A、B、C在运动的过程中,线段CB与AC相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,点A是x轴负半轴上一个定点,点P是函数
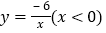 上一个动点,
上一个动点, 轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会
轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会


A. 先增后减 B. 先减后增 C. 逐渐减小 D. 逐渐增大
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B两地相距300千米,甲、乙两车同时从A地出发,以各自的速度匀速向B地行驶.甲车先到达B地,停留1小时后,速度不变,按原路返回.设两车行驶的时间是x小时,离开A地的距离是y千米,如图是y与x的函数图象.
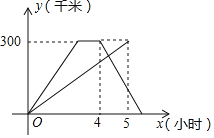
(1)甲车的速度是 ,乙车的速度是 ;
(2)甲车在返程途中,两车相距20千米时,求乙车行驶的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 的图象与反比例函数
的图象与反比例函数 的图象交于点
的图象交于点 ,C
,C ,交y轴于点B,交x轴于点D,那么不等式
,交y轴于点B,交x轴于点D,那么不等式 的解集是______ .
的解集是______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把
 的三边
的三边 、
、 和
和 分别向外延长一倍,将得到的点
分别向外延长一倍,将得到的点 、
、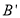 、
、 顺次连接成
顺次连接成 ,若
,若 的面积是5,则
的面积是5,则 的面积是( )
的面积是( )
A.15B.18C.21D.35
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=
 x+2的图象分别与坐标轴相交于A、B两点(如图所示),与反比例函数
x+2的图象分别与坐标轴相交于A、B两点(如图所示),与反比例函数 (x>0)的图象相交于C点.
(x>0)的图象相交于C点.(1)写出A、B两点的坐标;
(2)作CD⊥x轴,垂足为D,如果OB是△ACD的中位线,求反比例函数
 (x>0)的关系式.
(x>0)的关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=20°,∠ABC=30°.
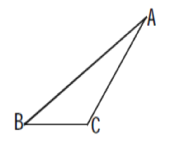
(1)画出BC边上的高AD和角平分线AE;
(2)求∠EAD的度数.
相关试题

