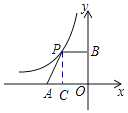
【题目】如图,平面直角坐标系中,点A是x轴负半轴上一个定点,点P是函数![]() 上一个动点,
上一个动点,![]() 轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会
轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会![]()
![]()

A. 先增后减 B. 先减后增 C. 逐渐减小 D. 逐渐增大
参考答案:
【答案】D
【解析】
过点P作PC⊥x轴于点C,根据k的几何意义可知矩形PBOC的面积为6,然后只需要讨论△APC的面积大小即可.
过点P作PC⊥x轴于点C,
∵点P在y=-![]() (x<0)
(x<0)
∴矩形PBOC的面积为6
设A的坐标为(a,0),P坐标(x,![]() )(x<0),
)(x<0),
△APC的面积为S,
当a<x<0时,
∴AC=x-a,
∴PC=-![]()
∴△APC的面积为S=![]() (x-a)
(x-a)![]() =-3(1-
=-3(1-![]() )
)
∵a<0,
∴-a>0,
∴-![]() 在a<x<0上随着x的增大而减小,
在a<x<0上随着x的增大而减小,
∴1-![]() 在a<x<0上随着x的增大而减小,
在a<x<0上随着x的增大而减小,
∴-3(1-![]() )在a<x<0上随着x的增大而增大,
)在a<x<0上随着x的增大而增大,
∴S=S△APC+6
∴S在a<x<0上随着x的增大而增大,
当x≤a时,
∴AC=a-x,
∴PC=-![]()
∴△APC的面积为S=![]() (a-x)
(a-x)![]() =-3(
=-3(![]() -1)
-1)
∵a<0,
∴![]() 在x<a随着x的增大而增大,
在x<a随着x的增大而增大,
∴![]() -1在x<a上随着x的增大而增大,
-1在x<a上随着x的增大而增大,
∴-3(![]() -1)在x<a上随着x的增大而减小,
-1)在x<a上随着x的增大而减小,
∴S=6-S△APC
∴S在x<a上随着x的增大而增大,
∴当P的横坐标增大时,S的值是逐渐增大,
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个边长分别为a,b(a>b)的正方形连在一起,三点C,B,F在同一直线上,反比例函数y=
 在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=10,则k的值是( )
在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=10,则k的值是( )
A. 3 B. 4 C. 5 D. 4

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知关于x的函数
 和
和 ,它们在同一坐标系内的图象大致是
,它们在同一坐标系内的图象大致是
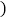
A.
 B.
B. 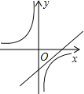 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平面直角坐标系xOy中,正比例函数y=kx与一次函数y=﹣x+b的图象相交于点A(4,3),过点P(2,0)作x轴的垂线,分别交正比例函数的图象于点B,交一次函数的图象与点C,连接OC.

(1)求这两个函数解析式;
(2)求△OBC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B两地相距300千米,甲、乙两车同时从A地出发,以各自的速度匀速向B地行驶.甲车先到达B地,停留1小时后,速度不变,按原路返回.设两车行驶的时间是x小时,离开A地的距离是y千米,如图是y与x的函数图象.
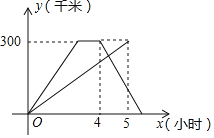
(1)甲车的速度是 ,乙车的速度是 ;
(2)甲车在返程途中,两车相距20千米时,求乙车行驶的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 的图象与反比例函数
的图象与反比例函数 的图象交于点
的图象交于点 ,C
,C ,交y轴于点B,交x轴于点D,那么不等式
,交y轴于点B,交x轴于点D,那么不等式 的解集是______ .
的解集是______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,一个点从数轴上的原点开始.先向左移动6cm到达A点,再从A点向右移动10cm到达B点,点C是线段AB的中点.
(1)点C表示的数是 ;
(2)若点A以每秒2cm的速度向左移动,同时C、B两点分别以每秒1cm、4cm的速度向右移动,设移动时间为t秒,
①运动t秒时,点C表示的数是 (用含有t的代数式表示);
②当t=2秒时,CBAC的值为 .
③试探索:点A、B、C在运动的过程中,线段CB与AC总有怎样的数量关系?并说明理由.

相关试题

