【题目】如图,在△ABC中,∠BAC=20°,∠ABC=30°.
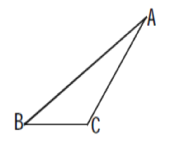
(1)画出BC边上的高AD和角平分线AE;
(2)求∠EAD的度数.
参考答案:
【答案】(1)见解析;(2)50°
【解析】
从三角形的一个顶点向它的对边作一条垂线,画出的这条线段就是三角形的高,注意钝角三角形较短边上的高在三角形的外部,再结合尺规作角平分线的方法即可解答第(1)问;
(2)根据已知条件,在△ABD中运用三角形内角和定理可得到∠BAD的度数,然后由角平分线的定义可得∠BAE=10°,再结合∠EAD=∠BAD-∠BAE即可得到答案.
(1)如图所示,AD为BC边上的高,AE为角平分线.
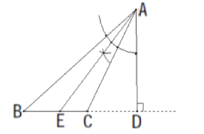
(2)∵AD⊥BD,
∴∠ADB=90°.
∵在△ABD中,∠ADB=90°,∠B=30°,
∴∠BAD=180°-90°-30°=60°.
∵∠BAC=20°,AE为∠BAC的平分线,
∴∠BAE=10°.
∵∠BAD=60°,∠BAE=10°,
∴∠EAD=∠BAD-∠BAE=60°-10°=50°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,一个点从数轴上的原点开始.先向左移动6cm到达A点,再从A点向右移动10cm到达B点,点C是线段AB的中点.
(1)点C表示的数是 ;
(2)若点A以每秒2cm的速度向左移动,同时C、B两点分别以每秒1cm、4cm的速度向右移动,设移动时间为t秒,
①运动t秒时,点C表示的数是 (用含有t的代数式表示);
②当t=2秒时,CBAC的值为 .
③试探索:点A、B、C在运动的过程中,线段CB与AC总有怎样的数量关系?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把
 的三边
的三边 、
、 和
和 分别向外延长一倍,将得到的点
分别向外延长一倍,将得到的点 、
、 、
、 顺次连接成
顺次连接成 ,若
,若 的面积是5,则
的面积是5,则 的面积是( )
的面积是( )
A.15B.18C.21D.35
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=
 x+2的图象分别与坐标轴相交于A、B两点(如图所示),与反比例函数
x+2的图象分别与坐标轴相交于A、B两点(如图所示),与反比例函数 (x>0)的图象相交于C点.
(x>0)的图象相交于C点.(1)写出A、B两点的坐标;
(2)作CD⊥x轴,垂足为D,如果OB是△ACD的中位线,求反比例函数
 (x>0)的关系式.
(x>0)的关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c是△ABC的三边长,且满足a2+2ab=c2+2bc,试判断这个三角形的形状.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
我们可以用配方法求一个二次三项式的最大值或最小值,例如:求代数式
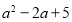 的最小值.方法如下:
的最小值.方法如下:解:
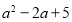
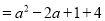
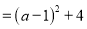
∵
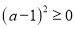 ,得
,得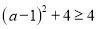 ,
,∴代数式
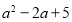 的最小值是4.
的最小值是4.请根据上述材料,解决下列问题:
(1)求代数式
 的最小值.
的最小值.(2)用配方法求代数式
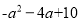 的最值.
的最值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
 ,OE平分
,OE平分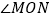 ,点A、B、C分别是射线OM、OE、ON上的动点
,点A、B、C分别是射线OM、OE、ON上的动点 、B、C不与点O重合
、B、C不与点O重合 ,连接AC交射线OE于点
,连接AC交射线OE于点 设
设 .
.
 如图1,若
如图1,若 ,则
,则 的度数是______;
的度数是______; 当
当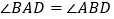 时,
时, ______;当
______;当 时,
时, ______.
______. 如图2,若
如图2,若 ,则是否存在这样的x的值,使得
,则是否存在这样的x的值,使得 中有两个相等的角?若存在,求出x的值;若不存在,说明理由.
中有两个相等的角?若存在,求出x的值;若不存在,说明理由.
相关试题

