【题目】观察下列两个等式:![]() ,
,![]() ,给出定义如下:我们称使等式
,给出定义如下:我们称使等式 ![]() 成立的一对有理数
成立的一对有理数![]() ,
,![]() 为“共生有理数对”,记为(
为“共生有理数对”,记为(![]() ,
,![]() ),如:数对(
),如:数对(![]() ,
,![]() ),(
),(![]() ,
,![]() ),都是“共生有理数对”.
),都是“共生有理数对”.
(1)数对(![]() ,
,![]() ),(
),(![]() ,
,![]() )中是“共生有理数对”吗?说明理由.
)中是“共生有理数对”吗?说明理由.
(2)若(![]() ,
,![]() )是“共生有理数对”,则(
)是“共生有理数对”,则(![]() ,
,![]() )是“共生有理数对”吗?说明理由.
)是“共生有理数对”吗?说明理由.
参考答案:
【答案】(1) (2,1)不是“共生有理数对”,![]() 是“共生有理数对”;理由见详解.
是“共生有理数对”;理由见详解.
(2) (n,m)是“共生有理数对”, 理由见详解.
【解析】
(1)根据“共生有理数对”的定义即可判断;
(2)根据“共生有理数对”的定义即可判断;
(1)21=3,2×1+1=1,
∴21≠2×1+1,
∴(2,1)不是“共生有理数对”,
∵![]()
∴![]()
∴![]() 是“共生有理数对”;
是“共生有理数对”;
(2)是.
理由: n (m)=n+m,
n(m)+1=mn+1
∵(m,n)是“共生有理数对”
∴mn=mn+1
∴n+m=mn+1
∴(n,m)是“共生有理数对”,
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点
 ,第二次点
,第二次点 跳动至点
跳动至点 第三次点
第三次点 跳动至点
跳动至点 ,第四次点
,第四次点 跳动至点
跳动至点 ……,依此规律跳动下去,则点
……,依此规律跳动下去,则点 与点
与点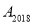 之间的距离是( )
之间的距离是( )
A. 2017B. 2018C. 2019D. 2020
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,第一次将
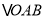 变换成
变换成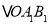 ,第二次将
,第二次将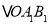 变换成
变换成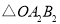 ,第三次将
,第三次将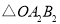 变换成
变换成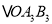 ,已知:
,已知: 、
、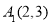 、
、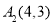 、
、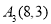 、
、 、
、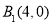
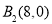 、
、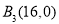 .若将
.若将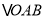 进行了
进行了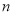 (
(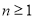 ,且
,且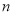 为整数)次变换,得到
为整数)次变换,得到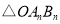 ,推测
,推测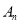 的坐标是_____,
的坐标是_____,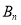 点的坐标是_______.
点的坐标是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△
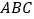 在平面直角坐标系中的位置如图所示.
在平面直角坐标系中的位置如图所示. (1)作出△
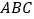 关于
关于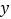 轴对称的△
轴对称的△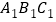 ,并写出△
,并写出△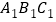 各顶点的坐标;
各顶点的坐标;(2)将△
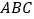 向右平移6个单位,作出平移后的△
向右平移6个单位,作出平移后的△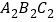 ,并写出△
,并写出△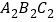 各顶点的坐标;
各顶点的坐标;(3)观察△
 和△
和△ ,它们是否关于某直线对称?若是,请用粗线条画出对称轴.
,它们是否关于某直线对称?若是,请用粗线条画出对称轴.
-
科目: 来源: 题型:
查看答案和解析>>【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
时间x(天)
1≤x<50
50≤x≤90
售价(元/件)
x+40
90
每天销量(件)
200﹣2x
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣1)2017﹣(﹣
 )﹣3+(cos68°﹣2)0+|4
)﹣3+(cos68°﹣2)0+|4 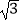 ﹣8sin60°|
﹣8sin60°| -
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD为矩形,G是BC上的任意一点,DE⊥AG于点E.
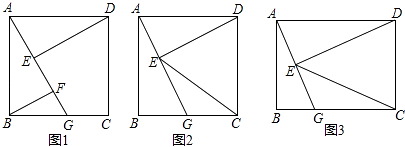
(1)如图1,若AB=BC,BF∥DE,且交AG于点F,求证:AF﹣BF=EF;
(2)如图2,在(1)条件下,AG=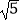 BG,求
BG,求 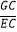 ;
;
(3)如图3,连EC,若CG=CD,DE=2,GE=1,则CE=(直接写出结果)
相关试题

