【题目】四边形ABCD为矩形,G是BC上的任意一点,DE⊥AG于点E.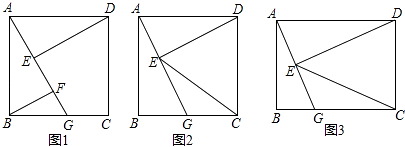
(1)如图1,若AB=BC,BF∥DE,且交AG于点F,求证:AF﹣BF=EF;
(2)如图2,在(1)条件下,AG= ![]() BG,求
BG,求 ![]() ;
;
(3)如图3,连EC,若CG=CD,DE=2,GE=1,则CE=(直接写出结果)
参考答案:
【答案】
(1)证明:∵四边形ABCD为矩形,AB=BC,
∴四边形ABCD为正方形,
∴AD=AB,∠BAD=90°,
又DE⊥AG,BF∥DE,
∴∠AED=∠AFB=90°,
∵∠BAF+∠DAE=90°,∠BAE+∠ABF=90°,
∴∠DAE=∠ABF,
在△AED和△BFA中,
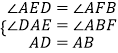
∴△AED≌△BFA(AAS),
∴AE=BF,
∴AF﹣BF=EF,
(2)解:如图2,延长AG与DC交于点F,
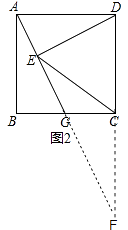
∵AG= ![]() BG,设BG=t,则AG=
BG,设BG=t,则AG= ![]() t,
t,
在Rt△ABG中,AB= ![]() =2t,
=2t,
∴G为BC的中点,
在△ABG和△FCG中,
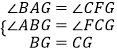
∴△ABG≌△FCG(AAS),
∴AB=FC=CD,
又∵DE⊥AG,
在Rt△DEF中,C为斜边DF的中点,
∴EC=CD=CF,
∴ ![]() =
= ![]() =
= ![]()
(3)![]()
【解析】解:(3)如图3,连接DG,作EM⊥BC于M点,

∵DE⊥AG,DE=2,GE=1,
∴在Rt△DEG中,DG= ![]() =
= ![]() =
= ![]() ,
,
∵CG=CD,
∴在Rt△DCG中,∠CDG=∠CGD=45°,
∴CD=CG= ![]() =
= ![]() ,
,
∵∠BAG+∠GAD=90°,∠EDA+∠GAD=90°,
∴∠BAG=∠EDA,
∵∠ABG=∠DEA=90°,
∴△ABG∽△DEA,
∴ ![]() =
= ![]() ,
,
设AD=x,则AE= ![]() =
= ![]() ,AG=
,AG= ![]() +1,
+1,
∴ ![]() =
= ![]() ,
,
解得x1= ![]() ,x2=﹣2
,x2=﹣2 ![]() (舍去)
(舍去)
∴AE= ![]() =
= ![]() ,
,
又∵∠BAG=∠MEG,
∴∠EDA=∠MEG,
∴△EMG∽△DEA
∴ ![]() =
= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() =
= ![]()
解得EM= ![]() ,MG=
,MG= ![]() ,
,
∴CM=CG+MG= ![]() +
+ ![]() =
= ![]() ,
,
∴CE= ![]() =
= ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对矩形的性质的理解,了解矩形的四个角都是直角,矩形的对角线相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列两个等式:
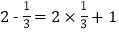 ,
,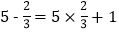 ,给出定义如下:我们称使等式
,给出定义如下:我们称使等式 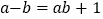 成立的一对有理数
成立的一对有理数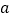 ,
,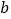 为“共生有理数对”,记为(
为“共生有理数对”,记为(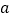 ,
,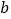 ),如:数对(
),如:数对(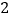 ,
, ),(
),(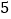 ,
, ),都是“共生有理数对”.
),都是“共生有理数对”.(1)数对(
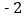 ,
,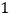 ),(
),(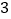 ,
, )中是“共生有理数对”吗?说明理由.
)中是“共生有理数对”吗?说明理由. (2)若(
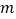 ,
,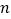 )是“共生有理数对”,则(
)是“共生有理数对”,则(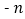 ,
,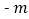 )是“共生有理数对”吗?说明理由.
)是“共生有理数对”吗?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
时间x(天)
1≤x<50
50≤x≤90
售价(元/件)
x+40
90
每天销量(件)
200﹣2x
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣1)2017﹣(﹣
 )﹣3+(cos68°﹣2)0+|4
)﹣3+(cos68°﹣2)0+|4 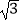 ﹣8sin60°|
﹣8sin60°| -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.

(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,点E在AD上,以BE为折痕将△ABE翻折,点A恰好落在CD边上的点F处. 已知△EDF的周长为12,△BCF的周长为22,求CF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】早晨小欣与妈妈同时从家里出发,步行与自行车向相反方向的两地上学与上班,如图是他们离家的路程
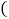 米
米 与时间
与时间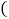 分钟
分钟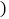 之间的函数图象,妈妈骑车走了10分钟时接到小欣的电话,立即以原速度返回并前往学校,若已知小欣步行的速度为50米
之间的函数图象,妈妈骑车走了10分钟时接到小欣的电话,立即以原速度返回并前往学校,若已知小欣步行的速度为50米 分钟,并且妈妈与小欣同时到达学校
分钟,并且妈妈与小欣同时到达学校 完成下列问题:
完成下列问题: 在坐标轴两处的括号内填入适当的数据;
在坐标轴两处的括号内填入适当的数据; 求小欣早晨上学需要的时间.
求小欣早晨上学需要的时间.
相关试题

