【题目】如图,已知直线y=3x﹣3分别交x轴,y轴于A,B两点,抛物线y=x2+bx+c经过A,B两点,点C是抛物线与x轴的另一个交点(与点A不重合),点D是抛物线的顶点,请解答下列问题. 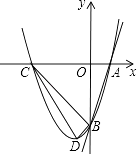
(1)求抛物线的解析式;
(2)判断△BCD的形状,并说明理由;
(3)求△BCD的面积.
参考答案:
【答案】
(1)解:∵直线y=3x﹣3分别交x轴,y轴于A,B两点,
当y=0时,x=1,当x=0时,y=﹣3,
∴点A(1,0),点B(0,﹣3),
∵抛物线y=x2+bx+c经过A,B两点,
∴ ![]() ,
,
解得, ![]() ,
,
∴抛物线的解析式为:y=x2+2x﹣3
(2)解:△BCD是直角三角形,
理由:∵y=x2+2x﹣3=(x+1)2﹣4=(x+3)(x﹣1),
∴当y=0时,x=﹣3或x=1,此抛物线的顶点坐标是(﹣1,﹣4),
∵抛物线y=x2+bx+c经过A,B两点,点C是抛物线与x轴的另一个交点(与点A不重合),点D是抛物线的顶点,
∴点C(﹣3,0),点D(﹣1,﹣4),
∵点B(0,﹣3),
∴BC= ![]() =3
=3 ![]() ,
,
CD= ![]() =2
=2 ![]() ,
,
BD= ![]() =
= ![]() ,
,
∵ ![]() ,
,
∴BC2+BD2=CD2,
∴△BCD是直角三角形
(3)解:由(2)知△BCD是直角三角形,∠CBD=90°, ![]() ,CD=2
,CD=2 ![]() ,BD=
,BD= ![]() ,
,
∴△BCD的面积是: ![]() ,
,
即△BCD的面积是3
【解析】(1)根据直线y=3x﹣3分别交x轴,y轴于A,B两点,可以求得点A和点B的坐标,由抛物线y=x2+bx+c经过A,B两点,从而可以得到抛物线的解析式;(2)根据(1)中的函数解析式可以分别求得点C和点D的坐标,从而可以求得BC、BD、CD的长,然后根据勾股定理的逆定理即可解答本题;(3)根据(2)中的判断,然后根据三角形的面积公式即可解答本题.
【考点精析】本题主要考查了抛物线与坐标轴的交点的相关知识点,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=10,AD=4,点P在边DC上,且△PAB是直角三角形,请在图中标出符合题意的点P,并直接写出PC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在长方形
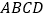 中,
中,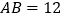 cm,
cm,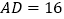 cm.现将其按下列步骤折叠:(1)将边
cm.现将其按下列步骤折叠:(1)将边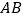 向边
向边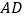 折叠,使边
折叠,使边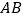 落在边
落在边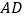 上,得到折痕
上,得到折痕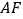 ,如图②;(2)将
,如图②;(2)将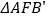 沿
沿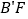 折叠,
折叠,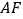 与
与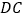 交于点
交于点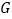 ,如图③.则所得梯形
,如图③.则所得梯形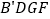 的周长等于( )
的周长等于( )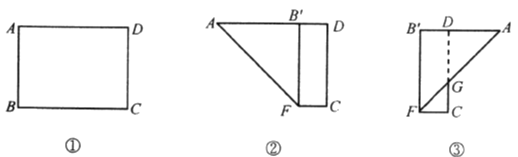
A.
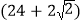 cm B.
cm B. 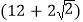 cm
cmC.
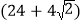 cm D.
cm D. 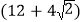 cm
cm -
科目: 来源: 题型:
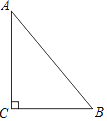
查看答案和解析>>【题目】如图是一块直角三角形的绿地,量得直角边BC为6cm,AC为8cm,现在要将原绿地扩充后成等腰三角形,且扩充的部分是以AC为直角边的直角三角形,求扩充后的等腰三角形绿地的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读:能够成为直角三角形三条边长的三个正整数a,b,c,称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其勾股数组公式为:
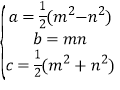 其中m>n>0,m,n是互质的奇数.
其中m>n>0,m,n是互质的奇数.应用:当n=1时,求有一边长为5的直角三角形的另外两条边长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意得( )
A.
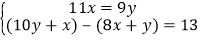 B.
B. 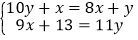
C.
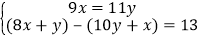 D.
D. 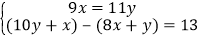
-
科目: 来源: 题型:
查看答案和解析>>【题目】菱形ABCD中,∠B=60°,∠MAN=60°,射线AM交直线BC于点E,射线AN交直线CD于点F,连结EF,请解答下列问题:
(1)如图1,求证:EC+FC=AC;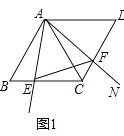
(2)将∠MAN绕点A旋转,如图2,如图3,请直接写出线段EC,FC,AC之间的数量关系,不需要证明;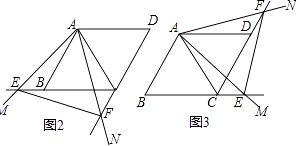
(3)若S菱形ABCD=18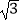 ,∠CAE=30°,则CF=
,∠CAE=30°,则CF=
相关试题

