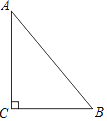
【题目】如图是一块直角三角形的绿地，量得直角边BC为6cm，AC为8cm，现在要将原绿地扩充后成等腰三角形，且扩充的部分是以AC为直角边的直角三角形，求扩充后的等腰三角形绿地的周长．

参考答案：

【答案】扩充后的等腰三角形绿地的周长为32m或（20+4）m或 m．

【解析】试题分析：根据题意画出图形，构造出等腰三角形，根据等腰三角形及直角三角形的性质利用勾股定理解答即可.

试题解析：在Rt△ABC中，∠ACB=90°，AC=8m，BC=6m，由勾股定理有：AB=10m，应分以下三种情况：

①如图1，

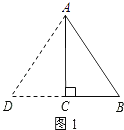
当AB=AD=10m时，

∵AC⊥BD，

∴CD=CB=6m，

∴△ABD的周长=10+10+2×6=32（m）．

②如图2，

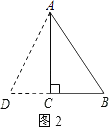
当AB=BD=10m时，

∵BC=6m，

∴CD=10﹣6=4m，

∴AD= ==4（m），

∴△ABD的周长=10+10+4=（20+4）m．

③如图3，

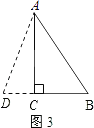
当AB为底时，设AD=BD=x，则CD=x﹣6，

∵由勾股定理得：AD2=AC2+CD2=82+（x﹣6）2=x2 ，

解得x=，

∴△ABD的周长为：AD+BD+AB=+ +10= （m）．

综上所述，扩充后的等腰三角形绿地的周长为：32m或（20+4）m或 m．

关闭