【题目】阅读下面解答过程,并填空或在括号内填写理由.
已知BE平分∠ABC交AC于点E,DE∥BC,且∠ABC=110°,![]() ,请说明BE⊥AC.
,请说明BE⊥AC.

解:∵![]() 平分
平分![]() (已知),
(已知),
∴∠EBC=![]() ∠_______(角平分线定义).
∠_______(角平分线定义).
∵![]() ,
,
∴∠EBC=_______![]() .
.
∵![]() ∥
∥![]() ,
,![]() (已知),
(已知),
∴∠EBC=∠_______(两直线平行,内错角相等),
∠C=∠AED=35° (________).
∴∠AEB=∠______+∠______=90°.
∴![]() .
.
参考答案:
【答案】∠ABC;55![]() ;∠DEB;两直线平行,同位角相等;∠AED;∠DEB
;∠DEB;两直线平行,同位角相等;∠AED;∠DEB
【解析】
根据角平分线的概念和平行线的性质,可求证∠AEB=90°,即BE⊥AC.
根据角平分线定义,以及“两直线平行,内错角相等”,“两直线平行,同位角相等”等概念和定理,即可得到答案.
解:∵![]() 平分
平分![]() (已知),
(已知),
∴∠EBC=![]() ∠__ABC_____(角平分线定义).
∠__ABC_____(角平分线定义).
∵![]() ,
,
∴∠EBC=___55____![]() .
.
∵![]() ∥
∥![]() ,
,![]() (已知),
(已知),
∴∠EBC=∠_DEB______(两直线平行,内错角相等),
∠C=∠AED=35° (___两直线平行,同位角相等_____).
∴∠AEB=∠__AED____+∠__DEB____=90°.
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列四种说法:①小明中途休息用了20分钟;②小明休息前爬山的平均速度为每分钟70米;③小明在上述过程中所走的路程为6600米;④小明休息前爬山的平均速度大于休息后爬山的平均速度.其中正确的是________(填序号).
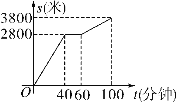
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下面的图象记录了某地一月份某大的温度随时间变化的情况,请你仔细观察图象回答下面的问题:

(1)在这个问题中,变量分别是______,时间的取值范围是______;
(2)20时的温度是______℃,温度是0℃的时刻是______时,最暖和的时刻是_______时,温度在-3℃以下的持续时间为______小时;
(3)你从图象中还能获得哪些信息?(写出1~2条即可)
答:__________________________________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,长方形ABCD的边BC平行于x轴,如果点A的坐标为(-1,2),点C的坐标为(3,-3),把一条长为2019个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按如图所示的逆时针方向绕在长方形ABCD的边上,则细线的另一端所在位置的点的坐标是( )

A. (-1,1)B. (-1,-1)C. (2,-2)D. (2,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数
 的图象与性质.小华根据学习函数的经验,对函数
的图象与性质.小华根据学习函数的经验,对函数 的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
的图象与性质进行了探究.下面是小华的探究过程,请补充完整:(1)在函数
 中,自变量x的取值范围是________.
中,自变量x的取值范围是________.x
…
-4
-3
-2
-1
0
1
2
3
4
…
y
…
5
4
3
2
1
0
1
2
m
…
①求m的值;
②在平面直角坐标系xOy中,描出以上表中各组对应值为坐标的点,并根据描出的点,画出该函数的图象.

(2)结合函数图象写出该函数的一条性质:________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)画出函数的图象;
(2)判断点


 是否在函数
是否在函数 的图象上;
的图象上;(3)若点
 在函数
在函数 的图象上,求出m的值.
的图象上,求出m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明每天上午9时骑自行车离开家,15时回家,他描绘了离家的距与时间的变化情况.

(1)图象表示哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和13时,他分别离家多远?
(3)他到达离家最远的地方时什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他由离家最远的地方返回的平均速度是多少.
相关试题

