搜索
【题目】小明每天上午9时骑自行车离开家，15时回家，他描绘了离家的距与时间的变化情况．
（1）图象表示哪两个变量的关系？哪个是自变量？哪个是因变量？
（2）10时和13时，他分别离家多远？
（3）他到达离家最远的地方时什么时间？离家多远？
（4）11时到12时他行驶了多少千米？
（5）他由离家最远的地方返回的平均速度是多少．
参考答案：
【答案】（1）图象表示了距离与时间，时间是自变量，距离是因变量．
（2）10时，他离家15千米，13时，他离家30千米；
（3）他到达离家最远的地方是12时，离家30千米；
（4）由图象可以看出从11时到12时他行驶了15千米；
（5）共用了2时，因此平均速度为30÷2=15千米/时．
【解析】解：（1）图象表示了距离与时间，时间是自变量，距离是因变量．
（2）10时，他离家15千米，13时，他离家30千米；
（3）他到达离家最远的地方是12时，离家30千米；
（4）由图象可以看出从11时到12时他行驶了15千米；
（5）共用了2时，因此平均速度为30÷2=15千米/时．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列命题中，真命题是( )
A. 两条对角线相等的四边形是矩形
B. 两条对角线互相垂直且平分的四边形是正方形
C. 等边三角形既是轴对称图形又是中心对称图形
D. 有一个角是60°的等腰三角形是等边三角形
-
科目： 来源： 题型：
查看答案和解析>>【题目】△ABC在方格中，位置如图，A点的坐标为（﹣3，1）．
（1）写出B、C两点的坐标；
（2）把△ABC向下平移1个单位长度，再向右平移2个单位长度，请你画出平移后的△A1B1C1；
（3）在x轴上存在点D，使△DB1C1的面积等于3，求满足条件的点D的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某弹簧的长度与所挂物体质量之间的关系如下表：
所挂物体的质量/千克
0
1
2
3
4
5
弹簧的长度/厘米
10
10.4
10.8
11.2
11.6
12
（1）如果所挂物体的质量用x表示，弹簧的长度用y表示，请直接写出y与x满足的关系式．
（2）当所挂物体的质量为10千克时，弹簧的长度是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】一水果贩子在批发市场按每千克1.8元批发了若干千克的西瓜进城出售，为了方便，他带了一些零钱备用．他先按市场价售出一些后，又降价出售．售出西瓜千克数x与他手中持有的钱数y元（含备用零钱）的关系如图所示，结合图象回答下列问题：
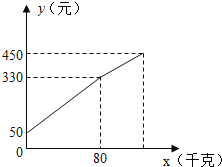
（1）农民自带的零钱是多少？
（2）降价前他每千克西瓜出售的价格是多少？
（3）随后他按每千克下降0.5元将剩余的西瓜售完，这时他手中的钱（含备用的钱）是450元，问他一共批发了多少千克的西瓜？
（4）请问这个水果贩子一共赚了多少钱？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，初三一班数学兴趣小组的同学欲测量公园内一棵树DE的高度，他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°．朝着这棵树的方向走到台阶下的点C处，测得树顶端D的仰角为60°，已知A点的高度AB为2米，台阶AC的坡度为1：
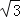（即AB：BC=1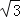：），且B，C，E三点在同一条直线上，请根据以上条件求出树DE的高度．（测量器的高度忽略不计）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图甲，点C将线段AB分成两部分（AC＞BC），如果
=
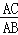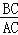，那么称点C为线段AB的黄金分割点．某数学兴趣小组在进行课题研究时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成面积分别为S1，S2（S1＞S2）的两部分，如果
=
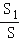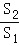，那么称直线l为该图形的黄金分割线．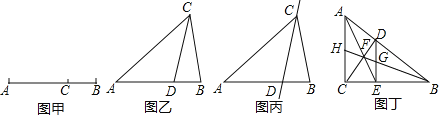
（1）如图乙，在△ABC中，∠A=36°，AB=AC，∠ACB的平分线交AB于点D，请问点D是否是AB边上的黄金分割点，并证明你的结论；
（2）若△ABC在（1）的条件下，如图丙，请问直线CD是不是△ABC的黄金分割线，并证明你的结论；
（3）如图丁，在Rt△ABC中，∠ACB=90°，D为斜边AB上的一点，（不与A，B重合）过D作DE⊥BC于点E，连接AE，CD相交于点F，连接BF并延长，与DE，AC分别交于点G，H．请问直线BH是直角三角形ABC的黄金分割线吗？并说明理由．
相关试题
