【题目】先阅读下面的内容,再解答问题.
(阅读)例题:求多项式m2 + 2mn+2n2-6n+13的最小值.
解;m2+2mn+2n2-6n+ 13= (m2 +2mn+n2)+ (n2-6n+9)+4= (m+n)2+(n-3)2+4,
∵(m+n)2![]() 0, (n-3)2
0, (n-3)2![]() 0
0
∴多项式m2+2mn+2n2-6n+ 13的最小值是4.
(解答问题)
(1)请写出例题解答过程中因式分解运用的公式是
(2)己知a、b、c是△ABC的三边,且满足a2+b2=l0a+8b-41,求第三边c的取值范围;
(3)求多项式-2x2+4xy-3y2 -3y2-6y+7 的最大值.
参考答案:
【答案】(1)完全平方公式;(2)1<c<9;(3)16
【解析】
(1)根据完全平方公式的特点求解;(2)配方可得(a-5)2+(b-4)2=0.求出a,b,可求出第三边取值范围;(3)运用完全平方公式,变形可得-2(x-y)2 -(y+3)2 +16,可求最大值.
解:(1)完全平方公式.
(2)∵a2 +b2 =10a+8b-41,∴a2-10a+25+b2-8b+16=0,
∴(a-5)2+(b-4)2=0.
∵(a-5)2≥0,(b-4)2≥0,∴a=5,b=4.
∴1<c<9.
(3)原式=-2x2+4xy-2y2 -y2-6y-9+16
=-2(x-y)2 -(y+3)2 +16,
∵-2(x-y)2≤0,-(y+3)2≤0,
∴ 多项式-2x2+4xy-3y2-6y+7 的最大值是 16.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若不等式3x<6的解都能使关于x的一次不等式(m-1)x<m+5成立,且使关于x的分式方程
 =
= 有整数解,那么符合条件的所有整数m的值之和是______.
有整数解,那么符合条件的所有整数m的值之和是______. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算或解方程:
(1)
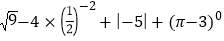
(2)
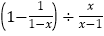
(3) 解方程:
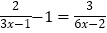
(4) 解方程:

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,点D、E分别在边AB、AC上,点F在CD上.
(1)若∠AED=∠ACB, ∠DEF= ∠B,求证:EF//AB;
(2)若D、E、F分别是AB、AC、CD的中点,连接BF,若四边形 BDEF的面积为6,试求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为3,E,F 分别是AB,BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM;
(2)当AE=1时,求EF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为丰富群众的业余生活并迎接社区文艺汇演,某小区特组建了一支“大妈广场舞队”(人数不超过50人).排练时,若排7排,则多3人;若排9排,且每排人数仅比排7 排时少1人,则最后-排不足6人.
(1)该“大妈广场舞队”共有多少名成员?
(2)为了提升表演效果,领队决定购买扇子和鲜花作为“大妈广场舞队”的表演道具.经预算,如果给40%的成员每人配1把扇子,其余的每人配1束鲜花,那么共需花费558元;如果 给60%的成员每人配1把扇子,其余的每人配1束鲜花,那么共需花费612元.问扇子和 鲜花的单价各是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x、y的二元一次方程组
 的解都为正数.
的解都为正数.(1)求a的取值范围;
(2)化简|a+1|﹣|a﹣1|;
(3)若上述二元一次方程组的解是一个等腰三角形的一条腰和一条底边的长,且这个等腰三角形的周长为9,求a的值.
相关试题

