搜索
【题目】计算或解方程：
(1)
(2) 
(3) 解方程: 
(4) 解方程: 
参考答案：
【答案】(1) -7；(2) 1；(3)
； (4)x =-1.
【解析】
（1）先化简各数，再根据有理数的加减法法则计算；
（2）先把括号里通分化简，再把除法转化为乘法约分化简；
（3）两边都乘以2(3x-1)，化为整式方程求解，求出x的值后检验即可；
（3）两边都乘以(x+2)(x-2)，化为整式方程求解，求出x的值后检验即可.
(1)
=3-4×4+5+1
=3-16+5+1
=-7；
(2) 
= 
=
×
=
×
=1；
(3) 
两边都乘以2(3x-1)，得
4-2(3x-1)=3，
解之得
，
经检验是分式方程的解；
(4) 
两边都乘以(x+2)(x-2)，得
4+(x+3)(x+2)= (x-1)(x-2)，
解之得
x =-1，
经检验x =-1是分式方程的解.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点A的坐标为(2,0)，等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD.
(1)△AOC沿x轴向右平移得到△OBD，则平移的距离是___个单位长度；△AOC与△BOD关于直线对称，则对称轴是___；△AOC绕原点O顺时针旋转得到△DOB，则旋转角度可以是___度；
(2)连结AD，交OC于点E，求∠AEO的度数。
-
科目： 来源： 题型：
查看答案和解析>>【题目】市煤气公司准备给某新建小区的用户安装管道煤气，现有
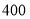用户提出了安装申请，此外每天还有新的用户提出申请，假设煤气公司每个安装小组安装的数量相同，且每天申请安装的用户数也相同，若煤气公司安排
个安装小组同时做，则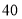
天就可以装完所有新、旧用户的申请；若煤气公司安排
个安装小组同时做，则
天可以装完所有新旧用户的申请.
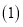求每天新申请安装的用户数及每个安装小组每天安装的数量；
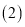如果要求在天内安装完所有新、旧用户的申请，但前
天煤气公司只能派出个安装小组安装，那么最后几天至少需要增加多少个安装小组同时安装，才能完成任务？ -
科目： 来源： 题型：
查看答案和解析>>【题目】若不等式3x＜6的解都能使关于x的一次不等式（m-1）x＜m+5成立，且使关于x的分式方程
=
有整数解，那么符合条件的所有整数m的值之和是______． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC中，点D、E分别在边AB、AC上，点F在CD上．
（1）若∠AED=∠ACB, ∠DEF= ∠B，求证：EF//AB；
（2）若D、E、F分别是AB、AC、CD的中点，连接BF，若四边形 BDEF的面积为6，试求△ABC的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】先阅读下面的内容，再解答问题．
（阅读）例题：求多项式m2 + 2mn+2n2-6n+13的最小值．
解；m2+2mn+2n2-6n+ 13= (m2 +2mn+n2)+ (n2-6n+9)+4= (m+n)2+(n-3)2+4，
∵(m+n)2
0, (n-3)20 ∴多项式m2+2mn+2n2-6n+ 13的最小值是4.
（解答问题）
（1）请写出例题解答过程中因式分解运用的公式是
（2）己知a、b、c是△ABC的三边，且满足a2+b2=l0a+8b-41，求第三边c的取值范围；
（3）求多项式－2x2＋4xy－3y2 －3y2－6y＋7 的最大值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD的边长为3，E，F 分别是AB，BC边上的点，且∠EDF=45°.将△DAE绕点D逆时针旋转90°，得到△DCM.
（1）求证：EF=FM；
（2）当AE=1时，求EF的长.
相关试题
