【题目】如图,已知△ABC中,点D、E分别在边AB、AC上,点F在CD上.
(1)若∠AED=∠ACB, ∠DEF= ∠B,求证:EF//AB;
(2)若D、E、F分别是AB、AC、CD的中点,连接BF,若四边形 BDEF的面积为6,试求△ABC的面积.

参考答案:
【答案】(1)详见解析;(2)16
【解析】
(1)根据平行线性质证出∠ADE=∠DEF,可得EF∥AB;(2)根据三角形中线把三角形面积平分性质求解.
(1)证明:∵∠AED=∠ACB,∴DE∥BC.∴∠ADE=∠B.
又∵∠DEF=∠B,∴∠ADE=∠DEF,∴EF∥AB.
(2)解:∵点 F 是DC的中点,∴设 S△DEF=S△CEF=x,
∵点E是AC的中点,∴S△ADE=S△CDE=2x,
∵点D是AB的中点,∴S△BDC=4x,S△BDF=2x,∴S 四边形 BDEF=3x.
∵S 四边形 BDEF=6,∴3x=6,∴x=2,∴S△ABC=8x=16.
-
科目: 来源: 题型:
查看答案和解析>>【题目】市煤气公司准备给某新建小区的用户安装管道煤气,现有
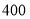 用户提出了安装申请,此外每天还有新的用户提出申请,假设煤气公司每个安装小组安装的数量相同,且每天申请安装的用户数也相同,若煤气公司安排
用户提出了安装申请,此外每天还有新的用户提出申请,假设煤气公司每个安装小组安装的数量相同,且每天申请安装的用户数也相同,若煤气公司安排 个安装小组同时做,则
个安装小组同时做,则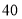 天就可以装完所有新、旧用户的申请;若煤气公司安排
天就可以装完所有新、旧用户的申请;若煤气公司安排 个安装小组同时做,则
个安装小组同时做,则 天可以装完所有新旧用户的申请.
天可以装完所有新旧用户的申请.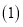 求每天新申请安装的用户数及每个安装小组每天安装的数量;
求每天新申请安装的用户数及每个安装小组每天安装的数量;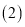 如果要求在
如果要求在 天内安装完所有新、旧用户的申请,但前
天内安装完所有新、旧用户的申请,但前 天煤气公司只能派出
天煤气公司只能派出 个安装小组安装,那么最后几天至少需要增加多少个安装小组同时安装,才能完成任务?
个安装小组安装,那么最后几天至少需要增加多少个安装小组同时安装,才能完成任务? -
科目: 来源: 题型:
查看答案和解析>>【题目】若不等式3x<6的解都能使关于x的一次不等式(m-1)x<m+5成立,且使关于x的分式方程
 =
= 有整数解,那么符合条件的所有整数m的值之和是______.
有整数解,那么符合条件的所有整数m的值之和是______. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算或解方程:
(1)
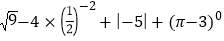
(2)
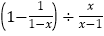
(3) 解方程:
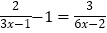
(4) 解方程:

-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面的内容,再解答问题.
(阅读)例题:求多项式m2 + 2mn+2n2-6n+13的最小值.
解;m2+2mn+2n2-6n+ 13= (m2 +2mn+n2)+ (n2-6n+9)+4= (m+n)2+(n-3)2+4,
∵(m+n)2
 0, (n-3)2
0, (n-3)2 0
0 ∴多项式m2+2mn+2n2-6n+ 13的最小值是4.
(解答问题)
(1)请写出例题解答过程中因式分解运用的公式是
(2)己知a、b、c是△ABC的三边,且满足a2+b2=l0a+8b-41,求第三边c的取值范围;
(3)求多项式-2x2+4xy-3y2 -3y2-6y+7 的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为3,E,F 分别是AB,BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM;
(2)当AE=1时,求EF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为丰富群众的业余生活并迎接社区文艺汇演,某小区特组建了一支“大妈广场舞队”(人数不超过50人).排练时,若排7排,则多3人;若排9排,且每排人数仅比排7 排时少1人,则最后-排不足6人.
(1)该“大妈广场舞队”共有多少名成员?
(2)为了提升表演效果,领队决定购买扇子和鲜花作为“大妈广场舞队”的表演道具.经预算,如果给40%的成员每人配1把扇子,其余的每人配1束鲜花,那么共需花费558元;如果 给60%的成员每人配1把扇子,其余的每人配1束鲜花,那么共需花费612元.问扇子和 鲜花的单价各是多少元?
相关试题

