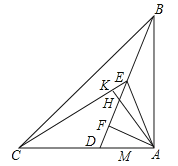
【题目】如图,在△ABC中,AC=AB,∠BAC=90°,D是AC边上一点,连接BD,AF⊥BD于点F,点E在BF上,连接AE,∠EAF=45°,连接CE,AK⊥CE于点K,交DE于点H,∠DEC=30°,HF=![]() ,则EC=______
,则EC=______
参考答案:
【答案】6
【解析】
延长AF交CE于P,证得△ABH≌△APC得出AH=CP,证得△AHF≌△EPF得出AH=EP,得出EC=2AH,解30°的直角三角形AFH求得AH,即可求得EC的长.
如图,延长AF交CE于P,
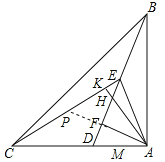
∵∠ABH+∠ADB=90°,∠PAC+∠ADB=90°,
∴∠ABH=∠PAC,
∵AK⊥CE,AF⊥BD,∠EHK=∠AHF,
∴∠HEK=∠FAH,
∵∠FAH+∠AHF=90°,∠HEK+∠EPF=90°,
∴∠AHF=∠EPF,
∴∠AHB=∠APC,
在△ABH与△APC中,
 ,
,
∴△ABH≌△APC(ASA),
∴AH=CP,
在△AHF与△EPF中,
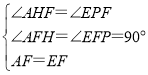 ,
,
∴△AHF≌△EPF(AAS),
∴AH=EP,∠CED=∠HAF,
∴EC=2AH,
∵∠DEC=30°,
∴∠HAF=30°,
∴AH=2FH=2×![]() =3,
=3,
∴EC=2AH=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,A点坐标为(-10,0),对角线AC和OB相交于点D且AC·OB=160.若反比例函数y=
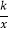 (x<0)的图象经过点D,并与BC的延长线交于点E,则S△OCE∶S△OAB=________.
(x<0)的图象经过点D,并与BC的延长线交于点E,则S△OCE∶S△OAB=________.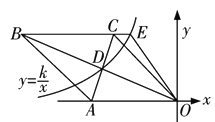
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠A=2∠C,BD平分∠ABC,BC=8,AB=5,则AD=________

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:
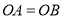 ,
,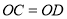 .
.
(1)请找出图中一对全等的三角形,并说明理由;
(2)若
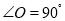 ,
,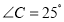 ,求
,求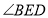 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题:
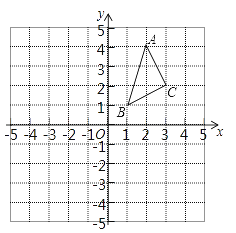
(1)①作出△ABC向左平移4个单位长度后得到的△A1B1C1, 并写出点C1的坐标;
②作出△ABC关于原点O对称的△A2B2C2, 并写出点C2的坐标;
(2)已知△ABC关于直线l对称的△A3B3C3的顶点A3的坐标为(-4,-2),请直接写出直线l的函数解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,点D、E分别在BC、AC上,且BD=CE,连接AD,BE交于点F;
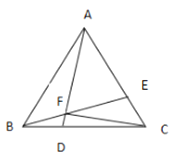
(1)求∠AFE的度数;
(2)连接FC,若∠AFC=90°,BF=1,求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时间,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是 米,小明在书店停留了 分钟
(2)本次上学途中,小明一共行驶了 米,一共用了 分钟.
(3)我们认为骑单车的速度超过300米分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?

相关试题

