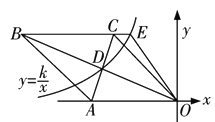
【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,A点坐标为(-10,0),对角线AC和OB相交于点D且AC·OB=160.若反比例函数y=![]() (x<0)的图象经过点D,并与BC的延长线交于点E,则S△OCE∶S△OAB=________.
(x<0)的图象经过点D,并与BC的延长线交于点E,则S△OCE∶S△OAB=________.
参考答案:
【答案】1:5
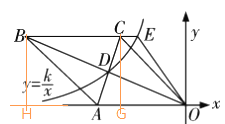
【解析】作CG⊥AO,BH⊥AO,根据菱形和三角形的面积公式可得S△OAC=![]() S菱形=40,从而得OA=10,CG=8,在Rt△OGE中,根据勾股定理得OG=6,AG=4,即C(-6,8),根据全等三角形的性质和中点坐标公式可得B(-16,8),D(-8,4),将D代入反比例函数解析式可得k,
S菱形=40,从而得OA=10,CG=8,在Rt△OGE中,根据勾股定理得OG=6,AG=4,即C(-6,8),根据全等三角形的性质和中点坐标公式可得B(-16,8),D(-8,4),将D代入反比例函数解析式可得k,
设E(a,8),将点E坐标代入反比例函数解析式,可得E(-4,8);根据三角形面积公式分别求得S△OCE和S△OAB , 从而得S△OCE:S△OAB.
作CG⊥AO,BH⊥AO,
∵BO·AC=160,
∴S菱形=![]() ·BO·AC=80,
·BO·AC=80,
∴S△OAC=![]() S菱形=40,
S菱形=40,
∴![]() ·AO·CG=40,
·AO·CG=40,
∵A(-10,0),
∴OA=10,
∴CG=8,
在Rt△OGE中,
∴OG=6,AG=4,
∴C(-6,8),
∵△BAH≌△COG,
∴BH=CG=8,AH=OG=6,
∴B(-16,8),
∵D为BO的中点,
∴D(-8,4),
又∵D在反比例函数上,
∴k=-8×4=-32,
∵C(-6,8),
∴E(a,8),
又∵E在反比例函数上,
∴8a=-32,
∴a=-4,
∴E(-4,8),
∴CE=2,
∴S△OCE=![]() ·CE·CG=
·CE·CG=![]() ×2×8=8,
×2×8=8,
S△OAB=![]() ·OA·BH=
·OA·BH=![]() ×10×8=40,
×10×8=40,
∴S△OCE:S△OAB=8:40=1:5.
故答案为:1:5.
-
科目: 来源: 题型:
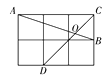
查看答案和解析>>【题目】如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点O,则tan∠AOD=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得的宽度,他们是这样做的:①在河流的一条岸边B点,选对岸正对的一棵树A;②沿河岸直走20m有一棵树C,继续前行20m到达D处;③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;④测得DE的长为5米.
(1)河的宽度是 米.
(2)请你说明他们做法的正确性.

-
科目: 来源: 题型:
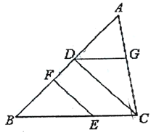
查看答案和解析>>【题目】将下面的证明过程补充完整,括号内写上相应理由或依据:已知,如图,
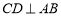 ,
, ,垂足分别为D、F,
,垂足分别为D、F,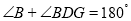 ,请试说明
,请试说明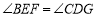 .
.
证明:∵
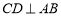 ,
, (已知)
(已知)∴
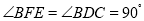 (____________________________)
(____________________________)∴
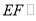 ________(____________________________)
________(____________________________)∴
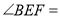 ________(____________________________)
________(____________________________)又∵
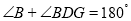 (已知)
(已知)∴
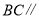 ________(____________________________)
________(____________________________)∴
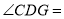 ________(____________________________)
________(____________________________)∴
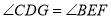 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠A=2∠C,BD平分∠ABC,BC=8,AB=5,则AD=________

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:
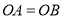 ,
,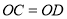 .
.
(1)请找出图中一对全等的三角形,并说明理由;
(2)若
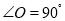 ,
,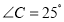 ,求
,求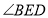 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=AB,∠BAC=90°,D是AC边上一点,连接BD,AF⊥BD于点F,点E在BF上,连接AE,∠EAF=45°,连接CE,AK⊥CE于点K,交DE于点H,∠DEC=30°,HF=
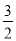 ,则EC=______
,则EC=______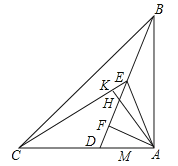
相关试题

