【题目】如图,在等边△ABC中,点D、E分别在BC、AC上,且BD=CE,连接AD,BE交于点F;
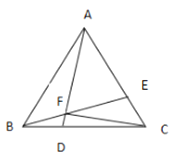
(1)求∠AFE的度数;
(2)连接FC,若∠AFC=90°,BF=1,求AF的长.
参考答案:
【答案】(1)60°;(2)2.
【解析】
(1)因为△ABC为等边三角形,所以∠ABD=∠BCE=60°,AB=AC=BC,又BD=CE,所以用“SAS”可判定△ABD≌△BCE,根据全等三角形的性质得出∠BAD=∠CBE,利用三角形外角性质解答即可;
(2)延长BE至H,使FH=AF,连接AH,CH,得到:△ACH,利用等边三角形的性质进而解答即可.
解:(1)∵△ABC为等边三角形,
∴AB=AC=BC,∠ABD=∠BCE=60°,
在△ABD和△BCE中,
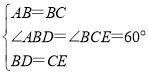 ,
,
∴△ABD≌△BCE(SAS);
∴∠BAD=∠CBE,
∵∠ADC=∠CBE+∠BFD=∠BAD+∠B,
∴∠BFD=∠B=∠AFE=60°;
(2)
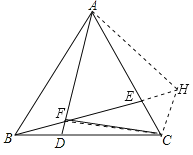
延长BE至H,使FH=AF,连接AH,CH
由(1)知∠AFE=60°,∠BAD=∠CBE,
∴△AFH是等边三角形,
∴∠FAH=60°,AF=AH,
∴∠BAC=∠FAH=60°,
∴∠BAC-∠CAD=∠FAH-∠CAD,
即∠BAF=∠CAH,
在△BAF和△CAH中,
∵AB=AC,∠BAF=∠CAH,AF=AH,
∴△BAF≌△CAH(SAS),
∴∠ABF=∠ACH,CH=BF=1;
又∵∠ABC=∠BAC,∠BAD=∠CBE,
∴∠ABC-∠CBE=∠BAC-∠BAD,
即∠ABF=∠CAF,
∴∠ACH=∠CAF,
∴AF∥CH,
∵∠AFC=90°,∠AFE=60°,
∴CF⊥CH,∠CFH=30°,
∴FH=2CH,
∴AF=2BF=2×1=2,
即AF的长为2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:
 ,
,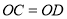 .
.
(1)请找出图中一对全等的三角形,并说明理由;
(2)若
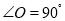 ,
,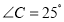 ,求
,求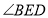 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=AB,∠BAC=90°,D是AC边上一点,连接BD,AF⊥BD于点F,点E在BF上,连接AE,∠EAF=45°,连接CE,AK⊥CE于点K,交DE于点H,∠DEC=30°,HF=
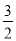 ,则EC=______
,则EC=______
-
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题:
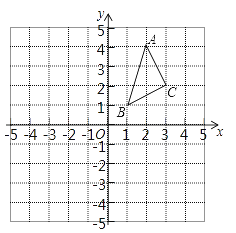
(1)①作出△ABC向左平移4个单位长度后得到的△A1B1C1, 并写出点C1的坐标;
②作出△ABC关于原点O对称的△A2B2C2, 并写出点C2的坐标;
(2)已知△ABC关于直线l对称的△A3B3C3的顶点A3的坐标为(-4,-2),请直接写出直线l的函数解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时间,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是 米,小明在书店停留了 分钟
(2)本次上学途中,小明一共行驶了 米,一共用了 分钟.
(3)我们认为骑单车的速度超过300米分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?

-
科目: 来源: 题型:
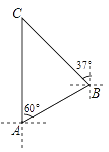
查看答案和解析>>【题目】知识改变世界,科技改变生活.导航装备的不断更新极大方便了人们的出行.如图,某校组织学生乘车到黑龙滩(用C表示)开展社会实践活动,车到达A地后,发现C地恰好在A地的正北方向,且距离A地13千米,导航显示车辆应沿北偏东60°方向行驶至B地,再沿北偏西37°方向行驶一段距离才能到达C地,求B、C两地的距离.(参考数据:sin53°≈
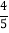 ,cos53°≈
,cos53°≈ ,tan53°≈
,tan53°≈ )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在△ABC中,BA=BC,BD是△ABC的中线,△ABC的角平分线AE交BD于点F,过点C作AB的平行线交AE的延长线于点G
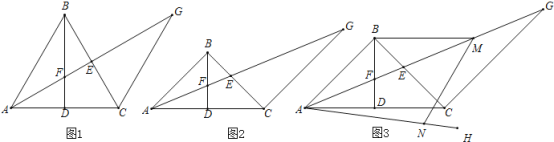
(1)如图1,若∠ABC=60°,求证:AF=
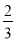 EG;
EG;(2)如图2,若∠ABC=90°,求证:AF=
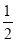 EG;
EG;(3)在(2)的条件下如图3,过点A作∠CAH=
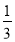 ∠FAC,过点B作BM∥AC交AG于点M,点N在AH上,连接MN、BN,若∠BMN+∠EAH=90°,
∠FAC,过点B作BM∥AC交AG于点M,点N在AH上,连接MN、BN,若∠BMN+∠EAH=90°,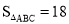 ,求BN的长.
,求BN的长.
相关试题

