【题目】“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时间,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是 米,小明在书店停留了 分钟
(2)本次上学途中,小明一共行驶了 米,一共用了 分钟.
(3)我们认为骑单车的速度超过300米分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?

参考答案:
【答案】(1)1500,4;(2)2700,14;(3)12到14分钟时速度最快,不在安全限度内
【解析】
(1)由y轴表示路程,起点是家,终点是学校,即可得到小明家到学校的路程是1500米,根据与x轴平行的线段表示路程没有变化,观察图象分析其对应的时间即可;
(2)行驶的路程=家到学校的距离+2![]() 折回书店的路程,时间=到学校的时间-从家出发的时间;
折回书店的路程,时间=到学校的时间-从家出发的时间;
(3)根据每一时间段所行驶的路程及时间,分别计算各时间段的速度进行比较即可.
(1)∵y轴表示路程,起点是家,终点是学校,
∴小明家到学校的路程是1500米,
由图象可知:小明在书店停留12-8=4分钟,
故答案为:1500,4;
(2)本次上学途中,小明行驶的路程=1500+2![]() (1200-600)=2700(米),
(1200-600)=2700(米),
一共用的时间=14-0=14(分钟),
故答案为:2700,14;
(3)0到6分钟时,平均速度=![]() (米/分),
(米/分),
6到8分钟时,平均速度=![]() (米/分),
(米/分),
12到14分钟时,平均速度=![]() (米/分)
(米/分)
∴12到14分钟时速度最快,不在安全限度内.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=AB,∠BAC=90°,D是AC边上一点,连接BD,AF⊥BD于点F,点E在BF上,连接AE,∠EAF=45°,连接CE,AK⊥CE于点K,交DE于点H,∠DEC=30°,HF=
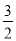 ,则EC=______
,则EC=______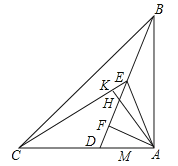
-
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题:
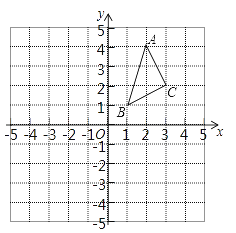
(1)①作出△ABC向左平移4个单位长度后得到的△A1B1C1, 并写出点C1的坐标;
②作出△ABC关于原点O对称的△A2B2C2, 并写出点C2的坐标;
(2)已知△ABC关于直线l对称的△A3B3C3的顶点A3的坐标为(-4,-2),请直接写出直线l的函数解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,点D、E分别在BC、AC上,且BD=CE,连接AD,BE交于点F;
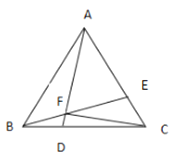
(1)求∠AFE的度数;
(2)连接FC,若∠AFC=90°,BF=1,求AF的长.
-
科目: 来源: 题型:
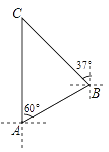
查看答案和解析>>【题目】知识改变世界,科技改变生活.导航装备的不断更新极大方便了人们的出行.如图,某校组织学生乘车到黑龙滩(用C表示)开展社会实践活动,车到达A地后,发现C地恰好在A地的正北方向,且距离A地13千米,导航显示车辆应沿北偏东60°方向行驶至B地,再沿北偏西37°方向行驶一段距离才能到达C地,求B、C两地的距离.(参考数据:sin53°≈
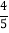 ,cos53°≈
,cos53°≈ ,tan53°≈
,tan53°≈ )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在△ABC中,BA=BC,BD是△ABC的中线,△ABC的角平分线AE交BD于点F,过点C作AB的平行线交AE的延长线于点G
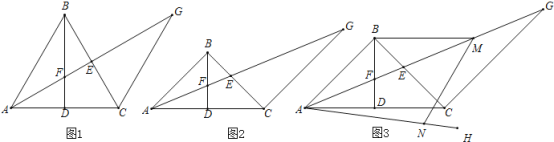
(1)如图1,若∠ABC=60°,求证:AF=
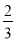 EG;
EG;(2)如图2,若∠ABC=90°,求证:AF=
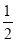 EG;
EG;(3)在(2)的条件下如图3,过点A作∠CAH=
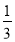 ∠FAC,过点B作BM∥AC交AG于点M,点N在AH上,连接MN、BN,若∠BMN+∠EAH=90°,
∠FAC,过点B作BM∥AC交AG于点M,点N在AH上,连接MN、BN,若∠BMN+∠EAH=90°,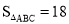 ,求BN的长.
,求BN的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料并解决后面的问题
材料:对数的创始人是苏格兰数学家纳皮尔(J.Npler,1550-1617年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evler,1707--1783)才发现指数与对数之间的联系,我们知道,n个相同的因数a相乘aa…,a记为an,如23=8,此时,3叫做以2为底8的对数,记为log28,即log28=3一般地若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab,即logab=n.如34=81,则4叫做以3为底81的对数,记为log381,即log381=4.
(1)计算下列各对数的值:log24=______,log216=______,log264=______;
(2)通过观察(1)中三数log24、log216、log264之间满足的关系式是______;
(3)拓展延伸:下面这个一股性的结论成立吗?我们来证明logaM+logaN=logaMN(a>0且a≠1,M>0,N>0)
证明:设logaM=m,logaN=n,
由对数的定义得:am=M,an=N,
∴aman=am+n=MN,
∴logaMN=m+n,
又∵logaM=m,logaN=n,
∴logaM+logaN=logaMN(a>0且a≠1,M>0,N>0);
(4)仿照(3)的证明,你能证明下面的一般性结论吗?logaM-logaN=loga
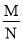 (a>0且a≠1,M>0,N>0)
(a>0且a≠1,M>0,N>0)(5)计算:log34+log39-log312的值为______.
相关试题

