【题目】在甲村至乙村的公路上有一块山地正在开发,现有一![]() 处需要爆破.已知点
处需要爆破.已知点![]() 与公路上的停靠站
与公路上的停靠站![]() 的距离为300米,与公路上的另一停靠站
的距离为300米,与公路上的另一停靠站![]() 的距离为400米,且
的距离为400米,且![]() ,如图所示为了安全起见,爆破点
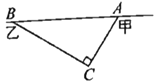
,如图所示为了安全起见,爆破点![]() 周围半径250米范围内不得进入,问在进行爆破时,公路
周围半径250米范围内不得进入,问在进行爆破时,公路![]() 段是否因为有危险而需要暂时封锁?请说明理由.
段是否因为有危险而需要暂时封锁?请说明理由.
参考答案:
【答案】公路![]() 段需要暂时封锁.理由见解析.
段需要暂时封锁.理由见解析.
【解析】
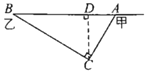
如图,本题需要判断点C到AB的距离是否小于250米,如果小于则有危险,大于则没有危险.因此过C作CD⊥AB于D,然后根据勾股定理在直角三角形ABC中即可求出AB的长度,然后利用三角形的公式即可求出CD,然后和250米比较大小即可判断需要暂时封锁.
公路![]() 段需要暂时封锁.理由如下:
段需要暂时封锁.理由如下:
如图,过点![]() 作
作![]() 于点
于点![]() .
.
因为![]() 米,
米,![]() 米,
米,![]() ,
,
所以由勾股定理知![]() ,即
,即![]() 米.
米.
因为![]() ,
,
所以![]() (米).
(米).
由于240米<250米,故有危险,因此公路![]() 段需要暂时封锁.
段需要暂时封锁.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.求证:(1)EC=BF;(2)EC⊥BF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2-2
 x+m=0有两个不相等的实数根.
x+m=0有两个不相等的实数根.(1)求实数m的最大整数值;
(2)在(1)的条件下,方程的实数根是x1,x2,求代数式
 +
+ -
- 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某同学上学期的数学历次测验成绩如下表所示:
测验类别
平时测验
期中测验
期末测验
第1次
第2次
第3次
成绩
100
106
106
105
110
(1)该同学上学期5次测验成绩的众数为 ,中位数为 ;
(2)该同学上学期数学平时成绩的平均数为 ;
(3)该同学上学期的总成绩是将平时测验的平均成绩、期中测验成绩、期末测验成绩按照2:3:5的比例计算所得,求该同学上学期数学学科的总评成绩(结果保留整数)。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,垂足分别为E、F,且AB=CD.

(1)△ABF与△CDE全等吗?为什么?
(2)求证:EG=FG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1所示,△ABC中,∠ACB的角平分线CF与∠EAC的角平分线AD的反向延长线交于点F;
①若∠B=90°则∠F= ;
②若∠B=a,求∠F的度数(用a表示);
(2)如图2所示,若点G是CB延长线上任意一动点,连接AG,∠AGB与∠GAB的角平分线交于点H,随着点G的运动,∠F+∠H的值是否变化?若变化,请说明理由;若不变,请求出其值.

-
科目: 来源: 题型:
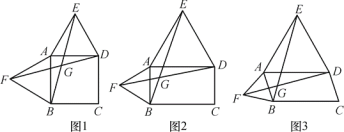
查看答案和解析>>【题目】以四边形ABCD的边AB,AD为边分别向外侧作等边△ABF和等边△ADE,连接EB,FD,交点为G.
(1)当四边形ABCD为正方形时(如图1),EB和FD的数量关系是 ;
(2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的数量关系?请加以证明;
(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由.
相关试题

