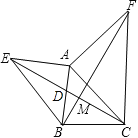
【题目】如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.求证:(1)EC=BF;(2)EC⊥BF.

参考答案:
【答案】见解析
【解析】
试题(1)先求出∠EAC=∠BAF,然后利用“边角边”证明△ABF和△AEC全等,根据全等三角形对应边相等即可证明;
(2)根据全等三角形对应角相等可得∠AEC=∠ABF,设AB、CE相交于点D,根据∠AEC+∠ADE=90°可得∠ABF+∠ADM=90°,再根据三角形内角和定理推出∠BMD=90°,从而得证.
证明:(1)∵AE⊥AB,AF⊥AC,
∴∠BAE=∠CAF=90°,
∴∠BAE+∠BAC=∠CAF+∠BAC,
即∠EAC=∠BAF,
在△ABF和△AEC中,
∵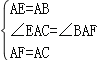 ,
,
∴△ABF≌△AEC(SAS),
∴EC=BF;
(2)如图,根据(1),△ABF≌△AEC,
∴∠AEC=∠ABF,
∵AE⊥AB,
∴∠BAE=90°,
∴∠AEC+∠ADE=90°,
∵∠ADE=∠BDM(对顶角相等),
∴∠ABF+∠BDM=90°,
在△BDM中,∠BMD=180°﹣∠ABF﹣∠BDM=180°﹣90°=90°,
所以EC⊥BF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知C是∠AOB的平分线上一点,点P,P′分别在边OA,OB上,如果要得到OP=OP′,需要添加以下条件中的某一个,那么所有可能结果的序号为________.
①∠OCP=∠OCP′;②∠OPC=∠OP′C;③PC=P′C;④PP′⊥OC.
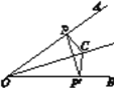
-
科目: 来源: 题型:
查看答案和解析>>【题目】从一个等腰三角形纸片的某角的顶点出发,能将其剪成两个等腰三角形纸片,则原等腰三角形纸片的底角为_______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小强掷两枚质地均匀的骰子,每个骰子的六个面上分别刻有1到6的点数,则两枚骰子点数相同的概率为
-
科目: 来源: 题型:
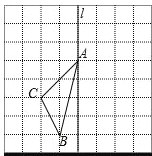
查看答案和解析>>【题目】如图,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)三角形ABC的面积为 ;
(3)在直线l上找一点P,使PB+PC的长最短.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠A=84°.
(1)试求作一点P,使得点P到B、C两点的距离相等,并且到AC、BC两边的距离也相等(尺规作图,不写作法,保留作图痕迹).
(2)在(1)的条件下,若∠ABP=15°,求∠BPC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰Rt△ABC中,∠C=90°,D为AC上一点,连接BD,将线段BD绕点D顺时针旋转90°得到线段DE,DE与AB相交于点F,过点D作DG⊥AB,垂足为点G.若EF=5,CD=2
 ,则△BDG的面积为 .
,则△BDG的面积为 . 
相关试题

