【题目】定义:有两条边长的比值为 ![]() 的直角三角形叫“潜力三角形”.如图,在△ABC中,∠B=90°,D是AB的中点,E是CD的中点,DF∥AE交BC于点F.
的直角三角形叫“潜力三角形”.如图,在△ABC中,∠B=90°,D是AB的中点,E是CD的中点,DF∥AE交BC于点F.
(1)设“潜力三角形”较短直角边长为a,斜边长为c,请你直接写出 ![]() 的值为;
的值为;
(2)若∠AED=∠DCB,求证:△BDF是“潜力三角形”;
(3)若△BDF是“潜力三角形”,且BF=1,求线段AC的长.
参考答案:
【答案】
(1)2或 ![]()
(2)
解:证明:延长AE交BC于G,如图所示:

∵DF∥AE,D是AB的中点,
∴∠AED=∠CDF,BF=GF,
∵∠AED=∠DCB,
∴∠CDF=∠DCB,
∴DF=CF,
∵DF∥AE,E是CD的中点,
∴CG=GF,
∴BF=GF=CG,
∴DF=CF=2GF=2BF,
∴ ![]() =
= ![]() ,
,
又∵∠B=90°,
∴△BDF是“潜力三角形”;
(3)
解:分四种情况:
①当 ![]() =
= ![]() 时,
时,
∵BF=1,
∴GF=CG=BF=1,BD=2,
∴AB=2BD=4,BC=3,
∴AC= ![]() =
= ![]() =5;
=5;
②当 ![]() =
= ![]() 时,DF=2BF=2,
时,DF=2BF=2,
∴BD= ![]() =
= ![]() =
= ![]() ,
,
∴AB=2BD=2 ![]() ,
,
∵BC=3,∠B=90°,
∴AC= ![]() =
= ![]() =
= ![]() ;
;
③当 ![]() =
= ![]() 时,BD=
时,BD= ![]() BF=
BF= ![]() ,
,
∴AB=2BD=1,
∵BC=3,∠B=90°,
∴AC= ![]() =
= ![]() =
= ![]() ;
;
④当 ![]() =
= ![]() 时,
时,
设BD=x,则DF=2x,
由勾股定理得:(2x)2﹣x2=12,
解得:x= ![]() ,
,
∴AB=2BD= ![]() ,
,
∵BC=3,∠B=90°,
∴AC= ![]() =
= ![]() =
= ![]() ;
;
综上所述:若△BDF是“潜力三角形”,且BF=1,线段AC的长为5或 ![]() 或
或 ![]() 或
或 ![]() .
.
【解析】(1)解:分两种情况:
①当 ![]() =
= ![]() 时,
时, ![]() =2;
=2;
②设另一条直角边长为b,当 ![]() =
= ![]() 时,b=2a,
时,b=2a,
∵∠B=90°,
∴c= ![]() =
= ![]() a,
a,
∴ ![]() =
= ![]() ;
;
所以答案是:2或 ![]() ;
;
【考点精析】通过灵活运用三角形的“三线”,掌握1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知y=﹣x+m(m>4)过动点A(m,0),并与反比例函数y=
 的图象交于B、C两点(点B在点C的左边),以OA为直径作反比例函数y=
的图象交于B、C两点(点B在点C的左边),以OA为直径作反比例函数y=  的图象相交的半圆,圆心为P,过点B作x轴的垂线,垂足为E,并于半圆P交于点D.
的图象相交的半圆,圆心为P,过点B作x轴的垂线,垂足为E,并于半圆P交于点D. 
(1)当m=5时,求B、C两点的坐标.
(2)求证:无论m取何值,线段DE的长始终为定值.
(3)记点C关于直线DE的对称点为C′,当四边形CDC′E为菱形时,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中∠C=90°,∠A=30°,BC=2,点P,Q,R分别是AB,AC,BC上的动点,PQ+PR+QR的最小值是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上一点.
(1)求证:AD2+DB2=ED2;
(2)若BC=
 ,求四边形ADCE的面积.
,求四边形ADCE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个同心圆的半径分别为4cm和5cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )

A.6cm
B.4cm
C.3cm
D.8cm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,E、F分别是CD、AB延长线上的点,连结EF,分别交AD、BC于点G、H.若∠1=∠2,∠A=∠C,试说明AD//BC和AB//CD.请完成下面的推理过程,填写理由或数学式:

∵∠1=∠2,∠1=∠AGH(_________)
∴∠2=∠AGH(________)
∴AD//BC(________)
∴∠ADE=∠C(________)
∵∠A=∠C(已知)
∴∠ADE=_______(等量代换)
∴AB//CD(_______)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
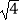 ﹣|﹣2|+(
﹣|﹣2|+(  )﹣2﹣20160 .
)﹣2﹣20160 .
相关试题

