【题目】已知抛物线y= ![]() x2﹣2x﹣1
x2﹣2x﹣1
(1)用配方法把抛物线化成顶点式,指出开口方向顶点坐标和对称轴
(2)用描点法画出图象. 
参考答案:
【答案】
(1)解:y= ![]() x2﹣2x﹣1,
x2﹣2x﹣1,
= ![]() (x2﹣4x+4)﹣
(x2﹣4x+4)﹣ ![]() ×4﹣1,
×4﹣1,
= ![]() (x﹣2)2﹣3;
(x﹣2)2﹣3;
∵a= ![]() >0,
>0,
∴开口方向:向上,
顶点坐标:(2,﹣3),
对称轴:x=2
(2)解:列表,
x | … | 0 | 1 | 2 | 3 | 4 | … |
y= | … | ﹣1 | ﹣2.5 | ﹣3 | ﹣2.5 | ﹣1 | … |
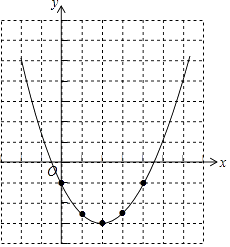
【解析】(1)根据配方法,先提取 ![]() ,然后利用完全平方公式整理即可,再根据a是正数以及顶点式形式分别求解即可;(2)根据二次函数图象的作法,列表、描点、连线画出图象即可.
,然后利用完全平方公式整理即可,再根据a是正数以及顶点式形式分别求解即可;(2)根据二次函数图象的作法,列表、描点、连线画出图象即可.
【考点精析】掌握二次函数的图象是解答本题的根本,需要知道二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果多边形的每个内角都比它相邻的外角的4倍多30°,求这个多边形的内角和及对角线的总条数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AD,那么添加下列一个条件后,能判定△ABC≌△ADC的是( )

A. AC=AC B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D
-
科目: 来源: 题型:
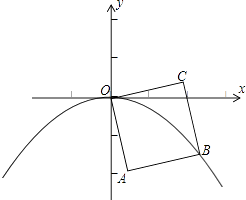
查看答案和解析>>【题目】如图,四边形OABC是边长为1的正方形,OC与x轴正半轴的夹角为15°,点B在抛物线y=ax2(a<0)的图象上,则a的值为
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C是
 的中点,CE⊥AB于E,BD交CE于点F.
的中点,CE⊥AB于E,BD交CE于点F. 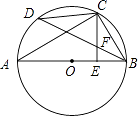
(1)求证:CF=BF;
(2)若CD=6,AC=8,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用长为28米长的篱笆围成一个矩形花园ABCD(篱笆只围AB、BC两边),设AB=x米,花园面积S.
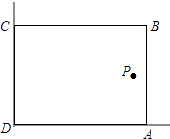
(1)写出S 关于x的函数解析式,当S=192平方米,求x的值;
(2)若在P处有一棵树与墙CD、AD的距离分别是15米和6米,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC是等腰三角形,AB=AC.
(1)特殊情形:如图1,当DE∥BC时,有DBEC.(填“>”,“<”或“=”)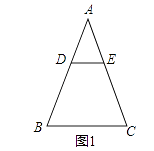
(2)发现探究:若将图1中的△ADE绕点A顺时针旋转α(0°<α<180°)到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.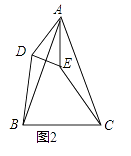
(3)拓展运用:如图3,P是等腰直角三角形ABC内一点,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度数.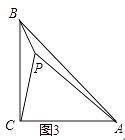
相关试题

