【题目】已知△ABC是等腰三角形,AB=AC.
(1)特殊情形:如图1,当DE∥BC时,有DBEC.(填“>”,“<”或“=”)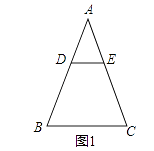
(2)发现探究:若将图1中的△ADE绕点A顺时针旋转α(0°<α<180°)到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.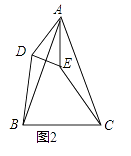
(3)拓展运用:如图3,P是等腰直角三角形ABC内一点,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度数.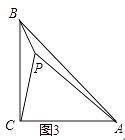
参考答案:
【答案】
(1)=
(2)
解:成立.
证明:由①易知AD=AE,
∴由旋转性质可知∠DAB=∠EAC,
在△DAB和△EAC中
得 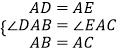
∴△DAB≌△EAC,
∴DB=CE
(3)
解:如图,
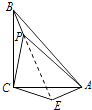
将△CPB绕点C旋转90°得△CEA,连接PE,
∴△CPB≌△CEA,
∴CE=CP=2,AE=BP=1,∠PCE=90°,
∴∠CEP=∠CPE=45°,
在Rt△PCE中,由勾股定理可得,PE=2 ![]() ,
,
在△PEA中,PE2=(2 ![]() )2=8,AE2=12=1,PA2=32=9,
)2=8,AE2=12=1,PA2=32=9,
∵PE2+AE2=AP2,
∴△PEA是直角三角形
∴∠PEA=90°,
∴∠CEA=135°,
又∵△CPB≌△CEA
∴∠BPC=∠CEA=135°
【解析】解:(1)∵DE∥BC,
∴ ![]() ,
,
∵AB=AC,
∴DB=EC,
故答案为:=,
(1)由DE∥BC,得到 ![]() ,结合AB=AC,得到DB=EC;(2)由旋转得到的结论判断出△DAB≌△EAC,得到DB=CE;(3)由旋转构造出△CPB≌△CEA,再用勾股定理计算出PE,然后用勾股定理逆定理判断出△PEA是直角三角形,在简单计算即可.
,结合AB=AC,得到DB=EC;(2)由旋转得到的结论判断出△DAB≌△EAC,得到DB=CE;(3)由旋转构造出△CPB≌△CEA,再用勾股定理计算出PE,然后用勾股定理逆定理判断出△PEA是直角三角形,在简单计算即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=
 x2﹣2x﹣1
x2﹣2x﹣1
(1)用配方法把抛物线化成顶点式,指出开口方向顶点坐标和对称轴
(2)用描点法画出图象.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C是
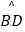 的中点,CE⊥AB于E,BD交CE于点F.
的中点,CE⊥AB于E,BD交CE于点F. 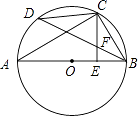
(1)求证:CF=BF;
(2)若CD=6,AC=8,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用长为28米长的篱笆围成一个矩形花园ABCD(篱笆只围AB、BC两边),设AB=x米,花园面积S.
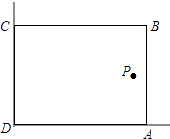
(1)写出S 关于x的函数解析式,当S=192平方米,求x的值;
(2)若在P处有一棵树与墙CD、AD的距离分别是15米和6米,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1抛物线y=ax2+bx+c过 A(﹣1,0)、B(4,0)、C(0,2)三点.
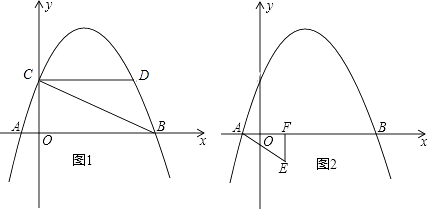
(1)求抛物线解析式;
(2)点C,D关于抛物线对称轴对称,求△BCD的面积;
(3)如图2,过点E(1,﹣1)作EF⊥x轴于点F,将△AEF绕平面内某点旋转180°得△MNQ(点M、N、Q分别与A、E、F对应)使得M、N在抛物线上,求M、N的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD纸片中,已知∠A=160°,∠B=30°,∠C=60°,四边形ABCD纸片分别沿EF,GH,OP,MN折叠,使A与A′、B与B′、C与C′、D与D′重合,则∠1+∠2+∠3+∠4+∠5+∠6+∠7﹣∠8的值是( )

A. 600° B. 700° C. 720° D. 800°
-
科目: 来源: 题型:
查看答案和解析>>【题目】从长度分别为3,5,6,9的四条线段中任取三条,能组成三角形的概率为( )
A.
B.
C.
D.
相关试题

