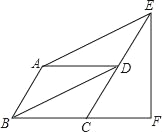
【题目】如图,平行四边形ABCD中,∠ABC=60°,点E、F分别在CD、BC的延长线上,AE∥BD,EF⊥BF,垂足为点F,DF=2.
(1)求证:D是EC中点;
(2)求EF的长.
参考答案:
【答案】(1)证明见解析;(2)2![]() .
.
【解析】
(1)根据平行四边形的对边平行可以得到AB∥CD,又AE∥BD,可以证明四边形ABDE是平行四边形,所以AB=DE,故D是EC的中点;
(2)连接DF,则△EFC是直角三角形,根据直角三角形斜边上的中线等于斜边的一半可以得到△CDF是等边三角形,根据勾股定理即可得到结论.
(1)证明:在平行四边形ABCD中,
AB∥CD,且AB=CD,
又∵AE∥BD,
∴四边形ABDE是平行四边形,
∴AB=DE,
∴CD=DE,
即D是EC的中点;
(2)解:∵EF⊥BF,
∴△EFC是直角三角形
又∵D是EC的中点,
∴DF=CD=DE=2,
∵AB∥CD,∠ABC=60°,
∴∠DCF=60°,
∴△DCF是等边三角形,
∴CF=2,
∴在Rt△ECF中
EF=![]() =
=![]() =2
=2![]() .
.
故答案为:(1)证明见解析;(2)2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.

(1)求证:△ABE≌△DAF;
(2)若AF=1,四边形ABED的面积为6,求EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c为非零的实数,则
 的可能值的个数为( )
的可能值的个数为( )A. 4 B. 5 C. 6 D. 7
-
科目: 来源: 题型:
查看答案和解析>>【题目】怡然美食店的A,B两种菜品,每份成本均为14元,售价分别为20元、18元,这两种菜品每天的营业额共为1120元,总利润为280元.
(1)该店每天卖出这两种菜品共多少份?
(2)该店为了增加利润,准备降低A种菜品的售价,同时提高B种菜品的售价,售卖时发现,A种菜品售价每降0.5元可多卖1份;B种菜品售价每提高0.5元就少卖1份,如果这两种菜品每天销售总份数不变,那么这两种菜品一天的总利润最多是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】某电器超市销售每台进价分别为2000元、1700元的A、B两种型号的空调,如表是近两周的销售情况:
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
5台
18000元
第二周
4台
10台
31000元
(进价、售价均保持不变,利润=销售总收入进货成本)
(1)求A、B两种型号的空调的销售单价;
(2)若超市准备用不多于54000元的金额再采购这两种型号的空调共30台,求A种型号的空调最多能采购多少台?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在八年级开展环保知识问卷调查活动,问卷一共10道题,八年级(三)班的问卷得分情况统计图如下图所示:

(1)扇形统计图中,a等于多少;
(2)根据以上统计图中的信息,①问卷得分的极差是多少分,②问卷得分的众数是多少分,③问卷得分的中位数是多少分;
(3)请你求出该班同学的平均分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我县某初中为了创建书香校园,购进了一批图书.其中的20本某种科普书和30本某种文学书共花了1080元,经了解,购买的科普书的单价比文学书的单价多4元.
(1)购买的科普书和文学书的单价各多少元?
(2)另一所学校打算用800元购买这两种图书,问购进25本文学书后至多还能购进多少本科普书?
相关试题

