【题目】如图,在△ABC中,∠ABC=90°,以BC为直径作⊙O,交AC于D,E为 ![]() 的中点,连接CE,BE,BE交AC于F.
的中点,连接CE,BE,BE交AC于F. 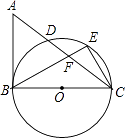
(1)求证:AB=AF;
(2)若AB=3,BC=4,求CE的长.
参考答案:
【答案】
(1)证明:∵E为 ![]() 的中点,
的中点,
∴ ![]() ,
,
∴∠DCE=∠CBE,
∵BC为⊙O的直径,
∴∠CEF=90°,
∴∠AFB=∠EFC=90°﹣∠DCE,
又∵∠ABF=∠ABC﹣∠CBE=90°﹣∠CBE,
∴∠ABF=∠AFB,
∴AB=AF;
(2)解:连接BD,如图所示:

∵BC为⊙O的直径,
∴∠BDC=90°,即BD⊥AC,
∵∠ABC=90°,
∴AC= ![]() =
= ![]() =5,
=5,
∵∠ADB=90°=∠ABC,∠A=∠A,
∴△ABD∽△ACB,
∴ ![]() =
= ![]() ,即
,即 ![]() ,
,
解得:AD= ![]() ,BD=
,BD= ![]() ,
,
∵AF=AB=3,
∴CF=AC﹣AF=2,DF=AF﹣AD=3﹣ ![]() =
= ![]() ,
,
∴BF= ![]() =
= ![]() ,
,
∵∠BDF=∠CEF,∠DFB=∠EFC,
∴△BDF∽△CEF,
∴ ![]() ,即
,即 ![]() ,
,
解得:CE= ![]() .
.
【解析】(1)由已知条件得出 ![]() ,由圆周角定理得出∠DCE=∠CBE,∠CEF=90°,得出∠AFB=∠EFC=90°﹣∠DCE,证出∠ABF=∠AFB,即可得出结论;(2)连接BD,由勾股定理求出AC=5,证明△ABD∽△ACB,得出对应边成比例求出AD=
,由圆周角定理得出∠DCE=∠CBE,∠CEF=90°,得出∠AFB=∠EFC=90°﹣∠DCE,证出∠ABF=∠AFB,即可得出结论;(2)连接BD,由勾股定理求出AC=5,证明△ABD∽△ACB,得出对应边成比例求出AD= ![]() ,BD=
,BD= ![]() ,由AF=AB=3,得出CF=AC﹣AF=2,DF=AF﹣AD=
,由AF=AB=3,得出CF=AC﹣AF=2,DF=AF﹣AD= ![]() ,由勾股定理求出BF,再证明△BDF∽△CEF,得出对应边成比例,即可得出结果.
,由勾股定理求出BF,再证明△BDF∽△CEF,得出对应边成比例,即可得出结果.
【考点精析】通过灵活运用圆周角定理和相似三角形的判定与性质,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为
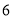 的正三角形纸片
的正三角形纸片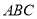 按如下顺序进行两次折叠,展开后,得折痕
按如下顺序进行两次折叠,展开后,得折痕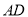 ,
,  (如图①),点
(如图①),点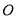 为其交点.
为其交点.(
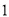 )探求
)探求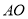 到
到 的数量关系,并说明理由.
的数量关系,并说明理由.(
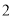 )如图②,若
)如图②,若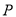 ,
, 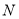 分别为
分别为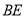 ,
, 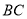 上的动点.
上的动点.①当
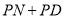 的长度取得最小值时,求
的长度取得最小值时,求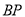 的长度.
的长度.②如图③,若点
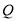 在线段
在线段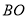 上,
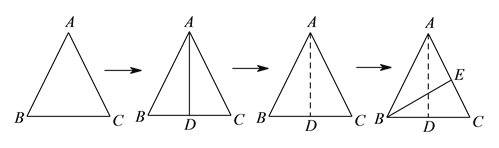
上, 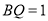 ,则
,则 的最小值
的最小值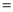 __________.
__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解题: 学习了二次根式后,你会发现一些含有根号的式子可以写成另一个式子的平方,如3+2
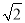 =(1+
=(1+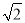 )2, 我们来进行以下的探索:
)2, 我们来进行以下的探索:设a+b
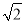 =(m+n
=(m+n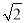 )2(其中a,b,m,n都是正整数),则有a+b
)2(其中a,b,m,n都是正整数),则有a+b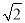 =m2+2n2+2mn
=m2+2n2+2mn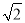 ,∴a=m+2n2 , b=2mn, 这样就得出了把类似a+b
,∴a=m+2n2 , b=2mn, 这样就得出了把类似a+b 的式子化为平方式的方法.
的式子化为平方式的方法.请仿照上述方法探索并解决下列问题:
(1)当a,b,m,n都为正整数时,若a﹣b
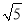 =(m﹣n
=(m﹣n )2 , 用含m,n的式子分别表示a,b,得a=________,b=________;
)2 , 用含m,n的式子分别表示a,b,得a=________,b=________; (2)利用上述方法,找一组正整数a,b,m,n填空:___﹣_____
 =(____﹣_____
=(____﹣_____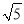 )2
)2 (3)a﹣4
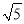 =(m﹣n
=(m﹣n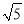 )2且a,m,n都为正整数,求a的值.
)2且a,m,n都为正整数,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b的图象经过点A(0,2)和点B(-a,3),且点B在正比例函数y=-3x的图象上.
(1)求a的值;
(2)求一次函数的解析式并画出它的图象;
(3)若P(m,y1),Q(m-1,y2)是这个一次函数图象上的两点,试比较y1与y2的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列多项式中,含有因式
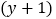 的多项式是( )
的多项式是( )A.
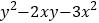 B.
B. 
C.
 D.
D. 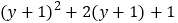
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
(1)(1+a)(1-a)+(a-2)2,其中a=
 ;
;(2)(2x+3)(2x-3)-4x(x-1)+(x-2)2,其中x=-3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,抛物线y=﹣x2﹣2x+3与x轴交于A,B两点(A在B的左侧),与y轴交于点C,顶点为D.

(1)请直接写出点A,C,D的坐标;
(2)如图(1),在x轴上找一点E,使得△CDE的周长最小,求点E的坐标;
(3)如图(2),F为直线AC上的动点,在抛物线上是否存在点P,使得△AFP为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.
相关试题

