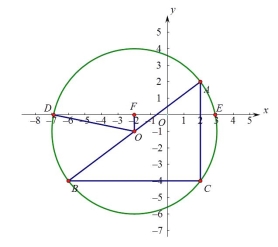
【题目】平面直角坐标系中,存在点A(2,2),B(-6,-4),C(2,-4).则△ABC的外接圆的圆心坐标为 , △ABC的外接圆在x轴上所截的弦长为 .
参考答案:
【答案】(-2,-1);![]()
【解析】在平面直角坐标中标出点A(2,2),B(-6,-4),C(2,-4),
可得![]() ABC是一个直角三角形,
ABC是一个直角三角形,
所以![]() ABC的外心O是AB的中点,则外心O的坐标为
ABC的外心O是AB的中点,则外心O的坐标为![]() , 即(-2,-1);
, 即(-2,-1);![]()
![]() 作OF
作OF![]() x轴,则外心到x轴的距离是OF=1,且
x轴,则外心到x轴的距离是OF=1,且![]() ABC的外接圆半径为
ABC的外接圆半径为![]() ,
,
则弦长DE=2×![]() .
.
所以答案是(-2,-1);4 ![]() .
.
【考点精析】本题主要考查了圆心角、弧、弦的关系和三角形的外接圆与外心的相关知识点,需要掌握在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心才能正确解答此题.
-
科目: 来源: 题型:
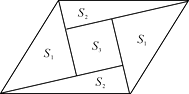
查看答案和解析>>【题目】如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1 , 另两张直角三角形纸片的面积都为S2 , 中间一张正方形纸片的面积为S3 , 则这个平行四边形的面积一定可以表示为( )
A.4S1
B.4S2
C.4S2+S3
D.3S1+4S3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
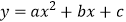 (
( 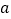 <
<  <0)与x轴最多有一个交点,现有以下结论:
<0)与x轴最多有一个交点,现有以下结论:
①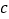 <0;②该抛物线的对称轴在y轴左侧;③关于x的方程
<0;②该抛物线的对称轴在y轴左侧;③关于x的方程 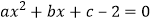 有实数根;④对于自变量x的任意一个取值,都有
有实数根;④对于自变量x的任意一个取值,都有 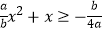 ,其中正确的为( )
,其中正确的为( )
A.①②
B.①②④
C.①②③
D.①②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程
 =2的解是负数,则n的取值范围为 .
=2的解是负数,则n的取值范围为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中画出两条相交直线y=x和y=kx+b,交点为(x0 , y0),在x轴上表示出不与x0重合的x1 , 先在直线y=kx+b上确定点(x1 , y1),再在直线y=x上确定纵坐标为y1的点(x2 , y1),然后在x轴上确定对应的数x2 , …,依次类推到(xn , yn-1),我们来研究随着n的不断增加,xn的变化情况.如图1(注意:图在下页上),若k=2,b=—4,随着n的不断增加,xn逐渐(填“靠近”或“远离”)x0;如图2,若k=
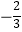 ,b=2,随着n的不断增加,xn逐渐(填“靠近”或“远离”)x0;若随着n的不断增加,xn逐渐靠近x0 , 则k的取值范围为 .
,b=2,随着n的不断增加,xn逐渐(填“靠近”或“远离”)x0;若随着n的不断增加,xn逐渐靠近x0 , 则k的取值范围为 . 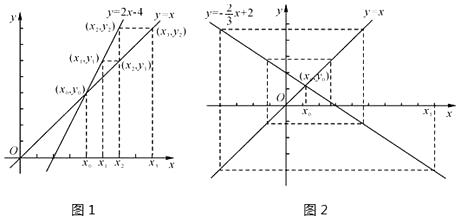
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣3)+7+(﹣6)+(﹣7)
(2)(-20)+(+3)-(-5)-(+7)
(3)(﹣3.5)×(﹣2)÷(-
 )÷(﹣5)
)÷(﹣5)(4)﹣14+16÷(﹣2)3×|﹣3﹣1|
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括O、B),做MN⊥DM,垂足为M,交∠CBE的平分线于点N.
(1)求点C的坐标;
(2)求证:MD=MN;
(3)如图(2),连接DN交BC于F,连接FM,探究线段MF、CF、OM之间有什么数量关系?并证明你的结论.
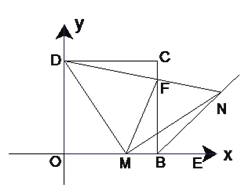
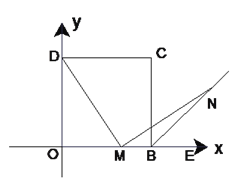
图(1) 图(2)
相关试题

