【题目】如图,平行四边形![]() 的对角线
的对角线![]() 、
、![]() 相交于点O,
相交于点O,![]() .
.
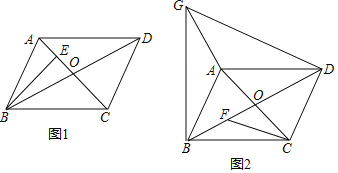
(1)如图1,过B作![]() 于E,若
于E,若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(2)如图2,若![]() ,过点C作
,过点C作![]() 交
交![]() 于点F,过点B作
于点F,过点B作![]() 且
且![]() ,连接
,连接![]() .求证:
.求证:![]() .
.
参考答案:
【答案】(1)![]() -4;(2)见解析.
-4;(2)见解析.
【解析】
(1)由勾股定理可求CE的长,由平行四边形的性质可得CO的长,即可求OE的长;
(2)延长CF交AB于点H,由“SAS”可证△ABG≌△FCB,可得AG=BF,由等腰三角形的性质可得AB=CD=2BH,再证明三角形BFH为等腰直角三角形,从而得出BF=![]() BH①;在Rt△CDF中,得出DF=
BH①;在Rt△CDF中,得出DF=![]() CD=
CD=![]() AB=2
AB=2![]() BH,继而得出OF=BO-BF=
BH,继而得出OF=BO-BF=![]() BH②,结合①②可得出结论.
BH②,结合①②可得出结论.
(1)解:∵BC=AC=8,BE=5,![]() ,
,
∴CE=![]() .
.
∵四边形ABCD是平行四边形,
∴AO=CO=4,
∴OE=EC-OC=![]() -4;
-4;
(2)证明:如图,延长CF交AB于点H,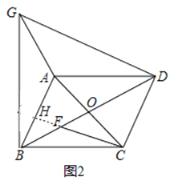
∵CF⊥CD,∠BDC=45°,
∴∠BDC=∠DFC=45°,
∴∠FBC+∠FCB=45°,CF=CD,
∵BC⊥BG,∠ABD=∠BDC=45°,
∴∠GBA+∠FBC=45°,
∴∠ABG=∠BCF,且AB=CD=CF,BC=BG,
∴△ABG≌△FCB(SAS),
∴AG=BF.
∵∠ABG+∠ABC=90°,∴∠BCF+∠ABC=90°,
∴CH⊥AB,又AC=BC,∴BH=AH,∴AB=CD=2BH.
∵AB∥CD,
∴∠ABF=∠CDB=45°,
∴∠HBF=∠BFH=45°,∴BH=FH,
∴BF=![]() BH①.
BH①.
在Rt△CDF中,CD=CF,∴DF=![]() CD=
CD=![]() AB=2
AB=2![]() BH,
BH,
∴BD=BF+DF=![]() BH +2
BH +2![]() BH=3
BH=3![]() BH,
BH,
∴BO=![]() BD=
BD=![]() BH,
BH,
∴OF=BO-BF=![]() BH②,
BH②,
∴由①②得,BF=2OF,
∴AG=2OF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校课外小组为了解同学们对学校“阳光跑操”活动的喜欢程度,抽取部分学生进行调查.被调查的每个学生按A(非常喜欢)、B(比较喜欢)、C(一般)、D(不喜欢)四个等级对活动评价.图1和图2是该小组采集数据后绘制的两幅统计图.经确认扇形统计图是正确的,而条形统计图尚有一处错误且并不完整.请你根据统计图提供的信息,解答下列问题:

(1)此次调查的学生人数为___;
(2)条形统计图中存在错误的是___(填A. B.C中的一个),并在图中加以改正;
(3)在图2中补画条形统计图中不完整的部分;
(4)如果该校有600名学生,那么对此活动“非常喜欢”和“比较喜欢”的学生共有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°,求大树的高度. (结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,
 ≈1.73)
≈1.73)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=115°,那么∠BFD的度数是
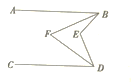
A.62°B.64°C.57.5°D.60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】某餐厅以
 、
、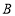 两种食材,利用不同的搭配方式推出了两款健康餐,其中,甲产品每份含200克
两种食材,利用不同的搭配方式推出了两款健康餐,其中,甲产品每份含200克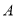 、200克
、200克 ;乙产品每份含200克
;乙产品每份含200克 、100克
、100克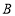 .甲、乙两种产品每份的成本价分别为
.甲、乙两种产品每份的成本价分别为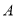 、
、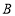 两种食材的成本价之和,若甲产品每份成本价为16元.店家在核算成本的时候把
两种食材的成本价之和,若甲产品每份成本价为16元.店家在核算成本的时候把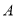 、
、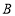 两种食材单价看反了,实际成本比核算时的成本多688元,如果每天甲销量的4倍和乙销量的3倍之和不超过120份,那么餐厅每天实际成本最多为______元.
两种食材单价看反了,实际成本比核算时的成本多688元,如果每天甲销量的4倍和乙销量的3倍之和不超过120份,那么餐厅每天实际成本最多为______元. -
科目: 来源: 题型:
查看答案和解析>>【题目】喜迎新中国70华诞,感受祖国70年沧桑巨变,70年壮丽辉煌,西大附中开展“祖国,我为你骄傲”的歌唱比赛,为了筹集歌唱比赛的演出服装资金,初二年级从批发市场购进
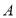 、
、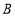 两种材料用于手工制作,进行“爱心义卖”.若每个
两种材料用于手工制作,进行“爱心义卖”.若每个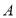 种材料的进价比每个
种材料的进价比每个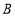 种材料的进价少2元,且用160元购进
种材料的进价少2元,且用160元购进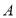 种材料的数量与用200元购进
种材料的数量与用200元购进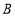 种材料的数量相等.
种材料的数量相等.(1)求
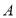 、
、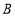 两种材料的进价分别为多少元?
两种材料的进价分别为多少元?(2)同学们齐心协力、大胆创新制作出了新颖别致的甲、乙两种手工艺品共56个,乙的数量比甲的数量的两倍还多,但多的个数不超过2个,甲的售价是24元/个,乙的售价是30元/个,为了使利润不低于1040元,有几种制作方案,哪种利润方案最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
= y2+8y+16 (第二步)
=(y+4)2 (第三步)
=(x2-4x+4)2 (第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 B.平方差公式 C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)
若不彻底,请直接写出因式分解的最后结果_________.
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
相关试题

